1) Hai người thợ quét sơn một ngôi nhà. Nếu họ cùng làm trong \[6\]ngày thì xong công việc. Hai người làm cùng nhau trong \[3\] ngày thì người thứ nhất được chuyển đi làm công việc khác, người thứ hai làm một mình trong \[4\] ngày nữa thì hoàn thành công việc. Hỏi nếu làm riêng thì mỗi người hoàn thành công việc đó trong bao lâu?
2) Bạn Mai làm một bài thi Toán gồm \[30\] câu trắc nghiệm, mỗi câu đúng được cộng \[4\] điểm, mỗi câu sai bị trừ \[1\] điểm, câu nào không làm thì không bị trừ và cũng không được cộng điểm. Bạn Mai đã làm \[25\] câu và đạt hơn \[82\] điểm. Hãy cho biết bạn Mai cần trả lời ít nhất bao nhiêu câu hỏi đúng để đạt được số điểm trên?
1) Hai người thợ quét sơn một ngôi nhà. Nếu họ cùng làm trong \[6\]ngày thì xong công việc. Hai người làm cùng nhau trong \[3\] ngày thì người thứ nhất được chuyển đi làm công việc khác, người thứ hai làm một mình trong \[4\] ngày nữa thì hoàn thành công việc. Hỏi nếu làm riêng thì mỗi người hoàn thành công việc đó trong bao lâu?
2) Bạn Mai làm một bài thi Toán gồm \[30\] câu trắc nghiệm, mỗi câu đúng được cộng \[4\] điểm, mỗi câu sai bị trừ \[1\] điểm, câu nào không làm thì không bị trừ và cũng không được cộng điểm. Bạn Mai đã làm \[25\] câu và đạt hơn \[82\] điểm. Hãy cho biết bạn Mai cần trả lời ít nhất bao nhiêu câu hỏi đúng để đạt được số điểm trên?
Quảng cáo
Trả lời:
1) Gọi \(x,y\) (ngày) lần lượt là thời gian người thứ nhất và người thứ hai làm một mình xong công việc (\(x,y > 6\)). Khi đó:
Trong một ngày người thứ nhất làm được \(\frac{1}{x}\) (công việc).
Trong một ngày người thứ hai làm được \(\frac{1}{y}\) (công việc).
Trong một ngày cả hai người làm được \(\frac{1}{6}\) (công việc) nên ta có phương trình: \(\frac{1}{x} + \frac{1}{y} = \frac{1}{6}\). (1)
Nếu người thứ nhất làm \(3\)ngày, người thứ hai làm \(7\)ngày thì họ làm xong việc nên ta có phương trình: \(\frac{3}{x} + \frac{7}{y} = 1\). (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{1}{6}\\\frac{3}{x} + \frac{7}{y} = 1\end{array} \right.\).
Đặt , \(b = \frac{1}{y}\), ta được: \(\left\{ \begin{array}{l}a + b = \frac{1}{6}\\3a + 7b = 1\end{array} \right.\,\,\,\,\,\,\,\,\,\,\)
\(\left\{ \begin{array}{l}7a + 7b = \frac{7}{6}\\3a + 7b = 1\end{array} \right.\,\,\,\,\,\,\,\,\,\,\)
\(\left\{ \begin{array}{l}4a = \frac{1}{6}\\a + b = \frac{1}{6}\end{array} \right.\,\,\,\,\,\,\,\,\,\,\)
\(\,\left\{ \begin{array}{l}a = \frac{1}{{24}}\\b = \frac{1}{{48}}\end{array} \right.\,\,\,\,\,\,\,\,\,\,\)
Mà \(a = \frac{1}{x}\), \(b = \frac{1}{y}\) nên:\(\,\,\left\{ \begin{array}{l}\frac{1}{x} = \frac{1}{{24}}\\\frac{1}{y} = \frac{1}{{48}}\end{array} \right.\,\,\,\,\,\,\,\,\) \(\,\,\,\left\{ \begin{array}{l}x = 24\\y = 48\end{array} \right.\) (thỏa mãn).
Vậy nếu làm một mình thì người thứ nhất hoàn thành công việc trong \(24\) ngày, người thứ hai hoàn thành công việc trong \(48\)ngày.
2) Gọi số câu trả lời đúng của bạn Mai là \(x\) (câu). ĐK \(x \in \mathbb{N}\,;\,\,x \le 25\)
Số câu trả lời sai của bạn Mai là \(25 - x\) (câu)
Số điểm được cộng khi trả lời đúng là \(4x\) (điểm)
Số điểm bị trừ khi trả lời sai là \(1\;{\rm{.}}\;\left( {25 - x} \right)\) (điểm)
Vì bạn Mai đã làm \[25\] câu và đạt hơn \[82\] điểm nên ta có \(4x - \left( {25 - x} \right) \ge 82\)
\(4x - 25 + x \ge 82\)
\(5x \ge 107\)
\(x \ge \frac{{107}}{5}\)
\(x \ge 21,4\)
Mà \(x \in \mathbb{N}\,;\,\,x \le 25\), \(x\) là số nhỏ nhất nên \(x = 22\)
Vậy bạn Mai cần trả lời ít nhất \(22\) câu hỏi đúng để đạt được số điểm trên \(82\) điểm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
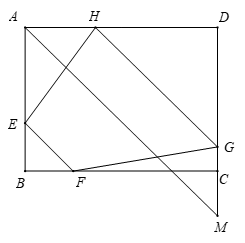
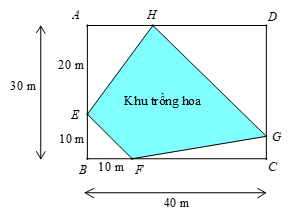
Gọi độ dài \(AH = x\,\left( {\rm{m}} \right)\) với \(0 < x < 40\). Khi đó \(HD = 40 - x\,\left( {\rm{m}} \right)\)
Qua \(A\) kẻ đường thẳng song song với \(EF\) cắt \(DC\) tại \(M\)
Khi đó \(\widehat {DHG} = \widehat {DAM} = \widehat {BEF} = 45^\circ \)
Do đó tam giác \(DHG\) vuông cân tại \(D\)
Suy ra \(DH = DG = 40 - x\,\left( {\rm{m}} \right)\)
Như vậy \(GC = DC - DG = 30 - \left( {40 - x} \right) = x - 10\,\left( {\rm{m}} \right)\)
Ta có: \({S_{AHE}} = \frac{1}{2}\, \cdot AH\, \cdot \,AE = \frac{1}{2}\, \cdot \,x \cdot 20 = 10x\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\)
\({S_{DHG}} = \frac{1}{2}\, \cdot DH\, \cdot DG = \frac{1}{2}\, \cdot \,{\left( {40 - x} \right)^2}\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\)
\({S_{FCG}} = \frac{1}{2}\, \cdot CG\, \cdot \,CF = \frac{1}{2}\, \cdot \,\left( {x - 10} \right)\, \cdot \,\left( {40 - 10} \right) = 15\left( {x - 10} \right)\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\)
\({S_{EFGH}} = {S_{ABCD}} - \left( {{S_{EBF}} + {S_{AEH}} + {S_{HDG}} + {S_{FGC}}} \right)\)
Đặt \(P = {S_{AEH}} + {S_{HDG}} + {S_{FGC}}\)
Ta cần tìm giá trị nhỏ nhất của \(P = 10x + \frac{{{{\left( {40 - x} \right)}^2}}}{2} + 15\left( {x - 10} \right)\)
\(P = 10x + \frac{{{x^2} - 80x + 1600}}{2} + 15x - 150\)
\(P = \frac{{{x^2}}}{2} - 15x + 650\)
\(2P = {x^2} - 30x + 1300\)
\[2P = {\left( {x - 15} \right)^2} + 1075 \ge 1075\]
Do đó \(P \ge 537,5\)
Dấu xảy ra khi \(x = 15\) (thỏa mãn điều kiện)
Vậy diện tích lớn nhất của mảnh đất trồng hoa là \(30\,.\,40 - \frac{1}{2}\, \cdot \,{10^2} - 537,5 = 612,5\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Lời giải
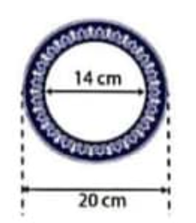
1) Bán kính lớn của viên trắng men xanh của đĩa sứ là \(20:2 = 10\) cm
Bán kính nhỏ của viên trắng men xanh của đĩa sứ là \(14:2 = 7\) cm
Diện tích phần viên trắng men xanh của đĩa sứ là
\(\pi ({R^2} - {r^2}) = \pi ({10^2} - {7^2}) \approx 160(c{m^2})\)
Vậy diện tích phần viên trắng men xanh của đĩa sứ khoảng \(160c{m^2}\)
2)
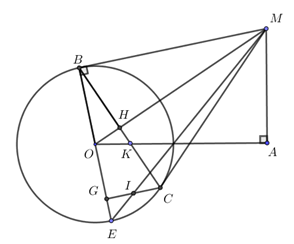
a) \(M,A,B,O\) cùng thuộc 1 đường tròn
\( \Rightarrow \Delta MAO\) vuông tại \(A\) \( \Rightarrow M,A,O\) thuộc đường tròn đường kính \(OM\) \((1)\)
\( \Rightarrow \Delta MBO\) vuông tại \(B\) \( \Rightarrow M,B,O\) thuộc đường tròn đường kính \(OM\) \((2)\)
Từ \((1),(2)\) \( \Rightarrow MABO\) cùng thuộc đường tròn đường kính \(OM\)
b) Xét \(\Delta MBO\) và \(\Delta MCO\) có:
\(MB = MC\) (\(M\) thuộc trung trực của \(BC\))
\(OB = OC( = R)\)
\( \Rightarrow \Delta MBO = \Delta MCO(c.c.c)\)
\( \Rightarrow MCO = MBO = 90^\circ \)
\( \Rightarrow MC \bot OC\) tại \(C \in (O)\)
\( \Rightarrow MC\) là tiếp tuyến của \((O)\)
• \((g.g)\) \( \Rightarrow \frac{{OK}}{{OM}} = \frac{{OH}}{{OA}}\) \( \Rightarrow OK \cdot OA = OH \cdot OM\)
• \((g.g)\) \( \Rightarrow \frac{{OH}}{{OB}} = \frac{{OB}}{{OM}}\) \( \Rightarrow OH \cdot OM = O{B^2} = {R^2}\)
\( \Rightarrow OK \cdot OA = OH \cdot OM = {R^2}\)
c) Vì \(GI\,{\rm{//}}\,BM\) \( \Rightarrow \frac{{BM}}{{GI}} = \frac{{BE}}{{GE}} \Rightarrow \frac{{BM}}{{2GI}} = \frac{{2BO}}{{2GE}} \Rightarrow \frac{{BM}}{{2GI}} = \frac{{BO}}{{GE}}(3)\)
(gg) \( \Rightarrow \frac{{BO}}{{GE}} = \frac{{BM}}{{GC}}\) (4)
Từ (3)(4) \( \Rightarrow \frac{{BM}}{{2GI}} = \frac{{BM}}{{GC}}\)\( \Rightarrow GC = 2GI\)\( \Rightarrow I\) là trung điểm của \(GC\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.