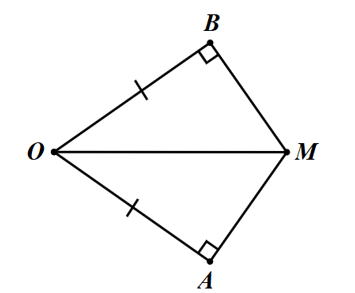
Cho \[\Delta ABC\] có \[\widehat B = \widehat C.\] Trên tia đối của tia \[BC\] lấy điểm \[M\], trên tia đối của tia \[CB\] lấy điểm \[N\] sao cho \[BM = CN.\] Kẻ \[AI \bot BC\,\,\,\left( {I \in BC} \right),\,\,BE \bot AM\,\,\left( {E \in AM} \right),\,\,CF \bot AN\,\,\left( {F \in AN} \right)\].
![Cho \[\Delta ABC\] có góc B = góc C.\] Trên tia đối của tia \[BC\] lấy điểm \[M\], trên tia đối của tia (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid10-1769100297.png)
Khi đó
Cho \[\Delta ABC\] có \[\widehat B = \widehat C.\] Trên tia đối của tia \[BC\] lấy điểm \[M\], trên tia đối của tia \[CB\] lấy điểm \[N\] sao cho \[BM = CN.\] Kẻ \[AI \bot BC\,\,\,\left( {I \in BC} \right),\,\,BE \bot AM\,\,\left( {E \in AM} \right),\,\,CF \bot AN\,\,\left( {F \in AN} \right)\].
![Cho \[\Delta ABC\] có góc B = góc C.\] Trên tia đối của tia \[BC\] lấy điểm \[M\], trên tia đối của tia (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid10-1769100297.png)
Khi đó
a) \[\widehat {ABM} = \widehat {ACN}\].
b) \[\Delta ABI = \Delta ACI\].
c) \[\Delta ABM = \Delta ANC.\]
Quảng cáo
Trả lời:
a) Đúng.
Nhận thấy, \[\widehat {ABM},\,\,\widehat {ACN}\] lần lượt kề bù với \[\widehat {ABC},\,\,\widehat {ACB}\].
Do đó, ta có: \[\widehat {ABM} = 180^\circ - \widehat {ABC},\,\,\widehat {ACN} = 180^\circ - \widehat {ACB}\].
Từ đó, suy ra \[\widehat {ABM} = \,\,\widehat {ACN}\].
b) Đúng.
Xét \[\Delta ABI\] và \[\Delta ACI\], có:
\[\widehat {ABI} = \widehat {ACI}\] (gt)
\[AI\] chung (gt)
Suy ra \[\Delta ABI = \Delta ACI\] (cạnh góc vuông – góc nhọn)
c) Sai.
Xét \[\Delta ABM\] và \[\Delta ACN\], có:
\[MB = NC\] (gt)
\[\widehat {MBA} = \widehat {NCA}\] (cmt)
\[AB = AC\,\,\left( {\Delta ABI = \Delta ACI} \right)\]
Do đó, \[\Delta ABM = \Delta ACN\] (c.g.c)
d) Đúng.
Vì \[\Delta ABM = \Delta ACN\] (cmt) nên \[\widehat {AMB} = \widehat {CNA}\] (hai góc tương ứng) hay \[\widehat {EMB} = \widehat {CNF}\].
Xét \[\Delta BME\] và \[\Delta CNF\] có:
\[MB = CN\] (gt)
\[\widehat {EMB} = \widehat {FNC}\] (cmt)
Do đó, \[\Delta BME = \Delta CNF\] (cạnh huyền – góc nhọn)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
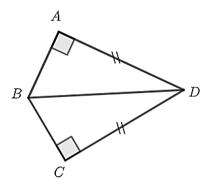
Xét \[\Delta BIM\] và \[\Delta CKM\] có:
\[MB = MC\] (\[M\] là trung điểm của \[BC\])
\[\widehat {BIM} = \widehat {CKM} = 90^\circ \].
\[\widehat {IMB} = \widehat {KMC}\] (đối đỉnh).
Do đó, \[\Delta BIM = \Delta CKM\] (cạnh huyền – góc nhọn)
Từ đó suy ra \[BI = CK\] (hai cạnh tương ứng).
Mà \[KC = 4\,\,{\rm{cm}}{\rm{.}}\]
Do đó, \[BI = 4\,\,{\rm{cm}}{\rm{.}}\]
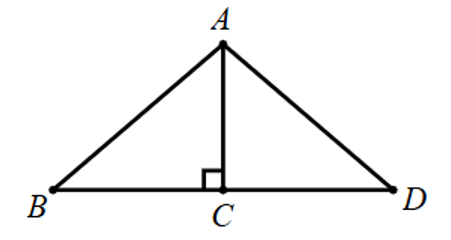
Lời giải
Xét hai tam giác vuông \[\Delta DAB\] và \[\Delta CAB\] có:
\[AD = AC\] (gt)
\[AB\] chung (gt)
Do đó, \[\Delta DAB = \Delta CAB\] (c.g.c)
Do đó, \[\widehat {BDA} = \widehat {ACB} = 30^\circ \] (hai góc tương ứng)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
a) \[\widehat {ACB} = 60^\circ \].
b) \[\Delta ABE = \Delta EBH.\]
c) \[BE\] là phân giác của \[\widehat B\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\widehat B = \widehat D.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Cạnh góc vuông – góc nhọn kề.
B. Cạnh – góc – cạnh.
C. Góc vuông – cạnh góc vuông.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho tam giác \[ABC,\,\,M\] là trung điểm của cạnh \[BC.\] Vẽ \[BI,\,\,CK\] vuông góc với \[AM.\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid15-1769100559.png)
![Tam giác \[ABC\] vuông tại \[A\] có góc C = 30 độ. Trên tia đối của tia \[AC\] lấy điểm \[D\] sao cho \[AD = AC\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid16-1769100600.png)