Cho cân tại \(A\) có \(AB = 5{\rm{ cm}}\). Khi đó:
Quảng cáo
Trả lời:
Đáp án đúng là: D
Ta có \(\Delta ABC\) cân tại \(A\) nên \(AB = AC = 5{\rm{ cm}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
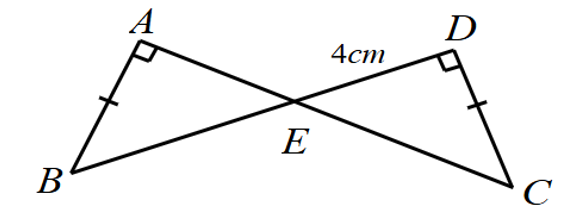
Xét \(\Delta ABE\) có \(\widehat A + \widehat B + \widehat {AEB} = 180^\circ \) (Định lí tổng ba góc trong một tam giác)
Suy ra \(\widehat B = 180^\circ - \widehat A - \widehat {AEB}\) (1)
Xét \(\Delta CED\) có \(\widehat C + \widehat D + \widehat {CED} = 180^\circ \) (Định lí tổng ba góc trong một tam giác)
Suy ra \(\widehat C = 180^\circ - \widehat D - \widehat {CED}\) (2)
Mà \(\widehat {AEB} = \widehat {CED}\) (Hai góc đối đỉnh) (3)
Từ (1), (2) và (3) suy ra \(\widehat B = \widehat C\).
Xét \(\Delta ABE\) và \(\Delta DCE\) có:
\(\widehat {BAC} = \widehat {BDC} = 90^\circ \)
\(AB = CD\)
\(\widehat B = \widehat C\)
Do đó, \(\Delta ABE = \Delta DCE\) (g.c.g)
Suy ra \(AE = DE\) (hai cạnh tương ứng)
Mà \(ED = 4{\rm{ cm}}\) nên \(EA = 4{\rm{ cm}}\).
Khoảng cách từ điểm \(E\) đến đường thẳng \(AB\) là \(EA\) (Vì \(AE \bot AB\) tại \(A\))
Vậy khoảng cách từ điểm \(E\) đến đường thẳng \(AB\) là \(4{\rm{ cm}}{\rm{.}}\)
Lời giải
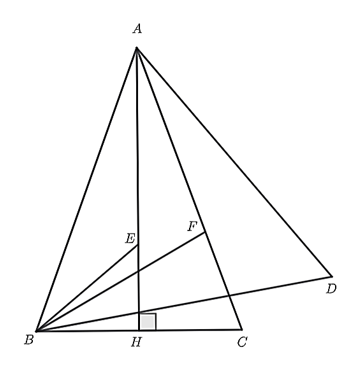
Vẽ \(\Delta ABD\) đều (\(B,D\) khác phía so với \(AC\)).
Ta có: \(\Delta ABC\) cân tại \(A,\) \(\widehat A = 40^\circ \) (gt)
Suy ra \(\widehat {ABC} = \widehat {ACB} = 70^\circ \) mà \(\widehat {FBC} = 30^\circ \) (gt)
Suy ra \(\widehat {ABF} = 40^\circ \), \(\widehat {BAF} = 40^\circ \) do đó \(\Delta ABF\) cân tại \(F.\)
Suy ra \(AF = BF\), mặt khác \(AB = BD\), \(FD\) chung
Do đó, \(\Delta AFB = \Delta BFD\) (c.c.c) nên \(\widehat {ADF} = \widehat {BDF} = \frac{{60^\circ }}{2} = 30^\circ \).
Do \(AH\) là đường cao của tam giác cân \(BAC.\)
Suy ra \(\widehat {BAE} = 20^\circ = \widehat {FAD} = 60^\circ - 40^\circ \), \(AB = AD\) (vì \(\Delta ABD\) đều), \(\widehat {ABE} = 30^\circ \) (gt)
Do đó, \(\Delta ABE = \Delta ADF\) (g.c.g)
Suy ra \(AE = AF\), do đó \(\Delta AEF\) cân tại \(A\) mà \(\widehat {EAF} = 20^\circ \).
Suy ra \(\widehat {AEF} = \frac{{120^\circ - 20^\circ }}{2} = 80^\circ \).Câu 3
a) \[\widehat {ABC} = \widehat {ACB}.\]
b) \[\widehat {{B_2}} = \widehat {{C_2}}\].
c) \[\Delta ABD = \Delta AEC\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho \[\Delta ABC\] cân tại \[A.\] Tia phân giác góc \[B\] cắt cạnh \[AC\] tại \[D\], tia phân giác góc \[C\] cắt cạnh \[AB\] tại \[E\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid3-1769140022.png)