Một đồ lưu niệm bằng thủy tinh có chiều cao bằng \(14\,(cm)\), được thiết kế gồm hai phần, phần dưới là một khối lập phương cạnh bằng \(8\,(cm)\) và phần trên là một phần của khối cầu có đường kính bằng \(8\,(cm)\) (được mô hình hóa bởi hình vẽ bên cạnh).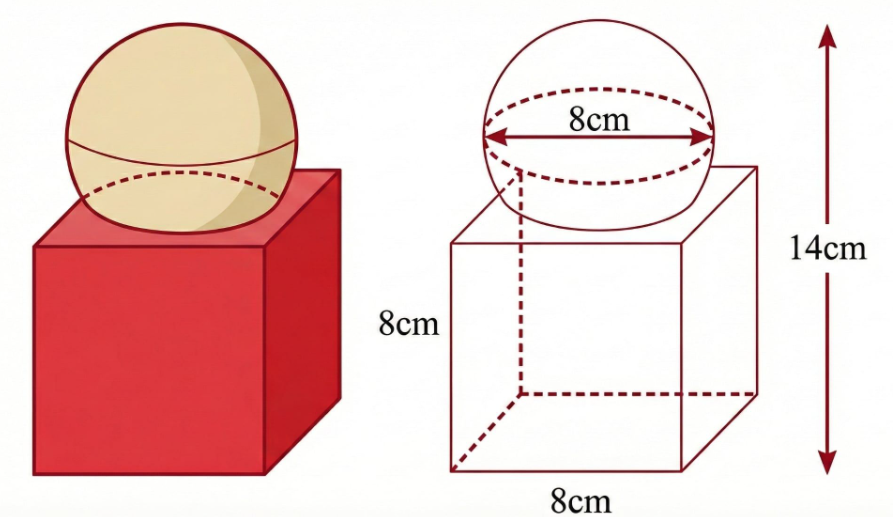
Quảng cáo
Trả lời:
a) Đúng
Thể tích của khối lập phương cạnh \(8\,(cm)\) bằng \(512\,(c{m^3})\).
b) Sai
Phần chỏm cầu có chiều cao bằng \(14 - 8 = 6\,(cm)\)
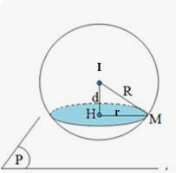
Mặt trên của hình lập phương cắt mặt cầu theo giao tuyến là đường tròn có bán kính bằng \(\sqrt {{4^2} - {{(6 - 4)}^2}} = 2\sqrt 3 \,(cm)\)
c) Sai
Ta tìm thể tích phần chỏm cầu phía dưới
Theo trên thì chỏm cầu phía dưới có chiều cao \(h' = 2\,(cm);\,r = 2\sqrt 3 \,(cm)\)
Vậy thể tích phần chỏm cầu phía dưới bằng \(V' = \pi {h^2}\left( {R - \frac{h}{3}} \right) = \pi {.2^2}\left( {4 - \frac{2}{3}} \right) = \frac{{40\pi }}{3}\,(c{m^3})\).
Ta có thể tích của khối cầu \(\frac{4}{3}\pi {.4^3} = \frac{{256\pi }}{3}\,(c{m^3})\).
Nên thể tích phần chỏm cầu phía trên bằng \(\frac{{256\pi }}{3} - \frac{{40\pi }}{3} = 72\pi \,(c{m^3})\).
d) Đúng
Thể tích của đồ lưu niệm đó là \(512\, + 72\pi \approx 738\,(c{m^3})\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
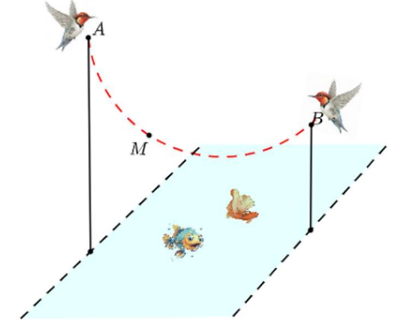
a) Đúng, Vì quỹ đạo bay của chim bói cá thuộc mặt phẳng vuông góc với mặt phẳng \(\left( {Oxy} \right)\) nên sẽ có phương trình là \(ax + by + c = 0\) (trong đó \(a,b\) không đồng thời bằng 0).
Vì mặt phẳng đi qua 2 điểm \(A(0;0;5)\) và \(B(4;0;4)\) nên ta có hệ \(\left\{ \begin{array}{l}c = 0\\4a + c = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}c = 0\\a = 0\end{array} \right.\)
Nên quỹ đạo bay của chim bói cá thuộc mặt phẳng \(y = 0\).
b) Sai, Đường tròn chứa quỹ đạo bay của chim bói cá có phương trình là \({x^2} + {z^2} - 2ax - 2bz + c = 0\) điều kiện \({a^2} + {b^2} - c > 0\).
Vì đường tròn đi qua các điểm \(A(0;0;5)\), \(B(4;0;4)\)nên ta có hệ phương trình
\(\left\{ \begin{array}{l}0a - 10b + c = - 25\\ - 8a - 8b + c = - 32\end{array} \right. \Rightarrow \left\{ \begin{array}{l}c = 10b - 25\\ - 8a + 2b = - 7\end{array} \right. \Rightarrow \left\{ \begin{array}{l}c = 10b - 25\\a = \frac{1}{4}b + \frac{7}{8}\end{array} \right.\).
Vì đường tròn đi qua điểm \(M\) thỏa mãn \(\widehat {AMB} = {135^ \circ }\) nên cung suy ra tam giác \(AIB\) vuông cân tại \(I\) suy ra \(R = \frac{{AB}}{{\sqrt 2 }} = \sqrt {\frac{{17}}{2}} \Rightarrow {a^2} + {b^2} - c = \frac{{17}}{2}\).
Suy ra \[{\left( {\frac{1}{4}b + \frac{7}{8}} \right)^2} + {b^2} - 10b + 25 = \frac{{17}}{2} \Rightarrow \frac{{17}}{{16}}{b^2} - \frac{{153}}{{16}}b + \frac{{1105}}{{64}} = 0 \Rightarrow \left[ \begin{array}{l}b = \frac{{13}}{2}\\b = \frac{5}{2}\end{array} \right.\].
Với \(b = \frac{{13}}{2}\) thì \(a = \frac{5}{2},c = 40\) đường tròn chứa quỹ đạo bay của chim bói cá có tâm \(I\left( {\frac{5}{2};0;\frac{{13}}{2}} \right).\)
Với \(b = \frac{5}{2}\) thì \(a = \frac{3}{2},c = 0\) đường tròn chứa quỹ đạo bay của chim bói cá có tâm \(I\left( {\frac{3}{2};0;\frac{5}{2}} \right).\)
Nhưng do đường tròn chứa cung như hình vẽ cao độ sẽ lớn hơn cao độ của điểm \(B\) nên ta nhận đường tròn chứa quỹ đạo bay của chim bói cá có tâm \(I\left( {\frac{5}{2};0;\frac{{13}}{2}} \right)\).
c) Đúng, Vì giao điểm của hai mặt phẳng \(\left( {Oxz} \right)\) và \(\left( {Oxy} \right)\) là trục \(Ox\) nên khoảng cách ngắn nhất mà chim bói cá bay xuống sát với mặt nước nhất là \(d = d\left( {I,Ox} \right) - R = \frac{{13}}{2} - \sqrt {\frac{{17}}{2}} \approx 3,58\,\left( {\rm{m}} \right)\).
d) Đúng, Điểm gần mặt nước nhất là điểm thấp nhất trên cung tròn (đỉnh vòm). Gọi là \(H\).
Ta cần tính độ dài cung\(AH\).
Xét tam giác \(IAH\) trong mặt phẳng quỹ đạo. \(I\left( {\frac{5}{2};0;\frac{{13}}{2}} \right),A\left( {0;0;5} \right)\)\( \Rightarrow \overrightarrow {IA} = \left( { - \frac{5}{2};0; - \frac{3}{2}} \right)\).
Vector chỉ hướng thẳng đứng xuống dưới từ tâm là \(\overrightarrow v = (0;0; - 1)\).
Góc quay \(\alpha \) từ \(A\) đến điểm thấp nhất \(H\) được tính qua cosin góc giữa \(IA\) và trục thẳng đứng: \(\cos \alpha = \frac{{\left| {{z_{IA}}} \right|}}{R} = \frac{{1,5}}{{\sqrt {\frac{{17}}{2}} }}\).
Suy ra \(\alpha = \arccos \left( {\frac{{1,5}}{{\sqrt {8,5} }}} \right) \approx 1,03{\mathop{\rm rad}\nolimits} \).
Độ dài cung \(L = R \cdot \alpha = \sqrt {8,5} \cdot 1,03 \approx 2,915 \cdot 1,03 \approx 3,00\;{\rm{m}}\).
Thời gian bay \(t = \frac{L}{v} = \frac{{3,00}}{2} = 1,5\) giây.
Lời giải
Đáp án: 37.
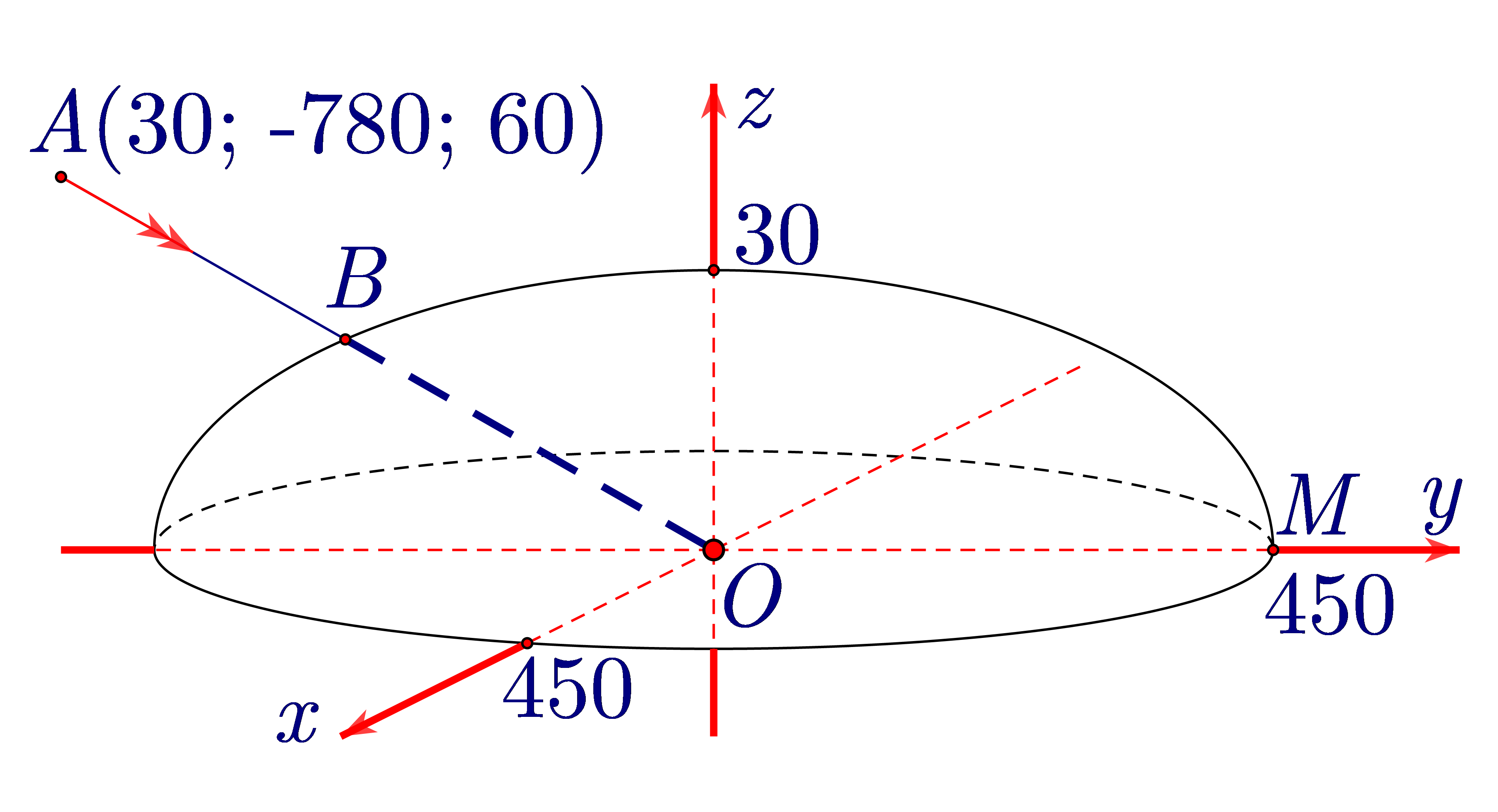
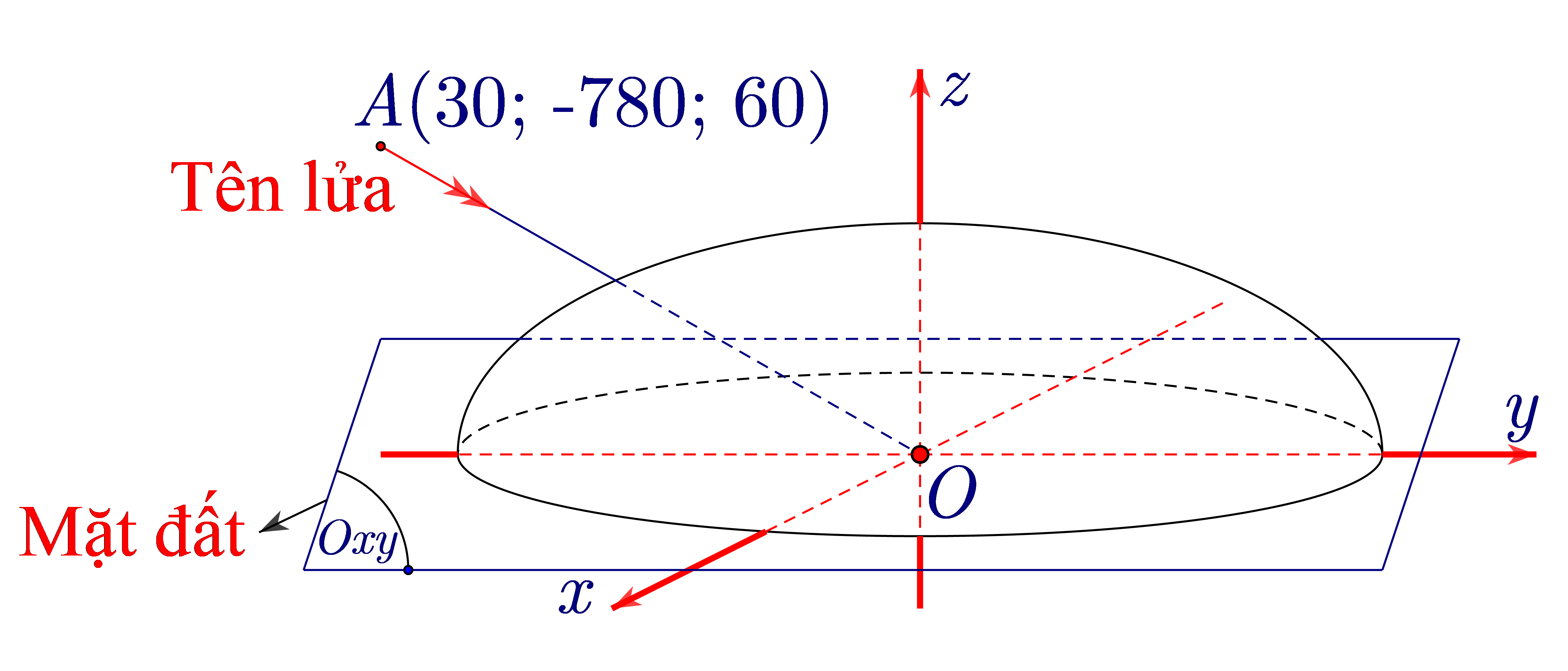
Gọi \(I\) là tâm của mặt cầu, \(M\) là giao điểm của đường tròn trên mặt đất với trục \(Oy.\) Khi đó
\(I{M^2} = {(IM - 30)^2} + {450^2} \Leftrightarrow IM = \frac{{{{30}^2} + {{450}^2}}}{{2.30}} = 3390{\rm{ km}}{\rm{.}}\)
Tọa độ tâm \(I\) là \(I(0;0; - 3360).\) Phương trình mặt cầu là \((S):{x^2} + {y^2} + {(z + 3360)^2} = {3390^2}.\)
Phương trình đường thẳng \(OA:\left\{ \begin{array}{l}x = 30t\\y = - 780t\\z = 60t\end{array} \right.\)
Gọi \(B = OA \cap (S)(AB < AO{\rm{ hay }}{z_B} > 0) \Rightarrow OB\) là đoạn đường tên lửa bay trong chỏm cầu.
Ta có phương trình
\({(30t)^2} + {( - 780t)^2} + {(60t + 3360)^2} = 11492100 \Leftrightarrow 612900{t^2} + 403200t - 202500 = 0\)
\( \Leftrightarrow \left[ \begin{array}{l}t = \frac{1}{3} \Rightarrow {B_1}\left( {10; - 260;20} \right)\left( {{z_{{B_1}}} > 0} \right)\\t = - \frac{{225}}{{227}} \Rightarrow {B_2}\left( { - \frac{{6750}}{{227}};\frac{{175500}}{{227}}; - \frac{{13500}}{{227}}} \right)\left( {{z_{{B_2}}} < 0} \right)\end{array} \right. \Rightarrow B(10; - 260;20)\)
Thời gian cần tìm là
\({t_{OB}} = \frac{{OB}}{7} = \frac{{\sqrt {{{10}^2} + {{( - 260)}^2} + {{20}^2}} }}{7} = \frac{{10\sqrt {681} }}{7} \approx 37{\rm{ (gi\^a y)}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.