Trong không gian \(Oxyz\), tính khoảng cách từ điểm \(M\left( {1;2; - 3} \right)\) đến mặt phẳng \(\left( P \right):\,x + 2y - 2z - 2 = 0\)
Quảng cáo
Trả lời:
Chọn C
\(d\left( {M,\left( P \right)} \right) = \frac{{\left| {\,1 + 2.2 - 2\left( { - 3} \right) - 2} \right|}}{{\sqrt {1 + 4 + 4} }} = 3\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
a) Đúng
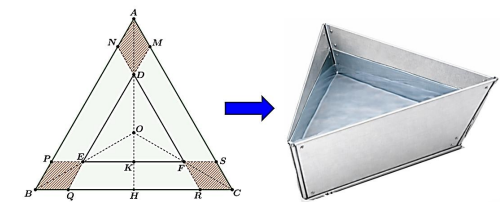
Ta có \(NP = QR = SM = AB - AN - BP = 6 - 2x\,(dm)\).
b) Đúng
Do tam giác \(ABC\) với cạnh bằng \(6\,dm\), nên \(AH = \sqrt {A{C^2} - C{H^2}} = 3\sqrt 3 \,(dm)\)
Và \(OA = \frac{2}{3}AH = 2\sqrt 3 \,(dm)\).
c) Đúng
Do \(AMDN\) là hình thoi cạnh \(x\) và \(\widehat {MAN} = {60^o}\),
Nên \(AD = \sqrt {A{N^2} + N{D^2} - 2AN.DN.cos{{120}^o}} = x\sqrt 3 \,(dm)\)
Lại có tam giác \(CMQ\) đều cạnh \(6 - x\,(dm)\)
Vậy \(DE = MQ - QE - DM = 6 - x - x - x = 6 - 3x\,(dm)\).
d) Đúng
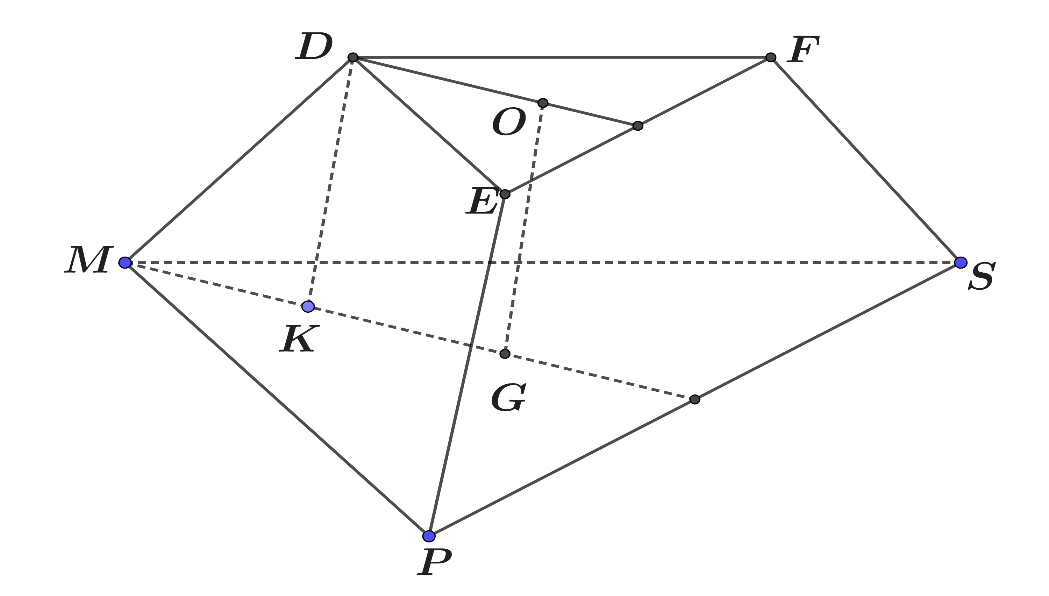
Ta có chóp cụt đều \(MPSDEF\) với cạnh đáy lớn \(MP = 6 - 2x\) và cạnh đáy nhỏ là \(DE = 6 - 3x\)
+) Ta có \({S_1} = {S_{DEF}} = \frac{{{{(6 - 3x)}^2}\sqrt 3 }}{4}\,(d{m^2})\).
+) Ta có \({S_2} = {S_{MPS}} = \frac{{{{(6 - 2x)}^2}\sqrt 3 }}{4}\,(d{m^2})\).
+) Ta có \(\sqrt {{S_1}{S_2}} = \sqrt {\frac{{{{(6 - 2x)}^2}\sqrt 3 }}{4} \times \frac{{{{(6 - 3x)}^2}\sqrt 3 }}{4}} = \frac{{(6 - 3x)(6 - 2x)\sqrt 3 }}{4}\,(d{m^2})\).
Kẻ \(DK \bot MG\,(K \in MG)\).
Ta tính \(h = OG = DK = \sqrt {M{D^2} - M{K^2}} \)
+) Ta có \(MD = x,\,\,MK = MG - KG = MG - DO = \frac{2}{3}\left( {6 - 2x} \right).\frac{{\sqrt 3 }}{2} - \frac{2}{3}\left( {6 - 3x} \right).\frac{{\sqrt 3 }}{2} = \frac{{x\sqrt 3 }}{3}\)\( \Rightarrow h = OG = \sqrt {{x^2} - {{\left( {\frac{{x\sqrt 3 }}{3}} \right)}^2}} = \frac{{x\sqrt 6 }}{3}\,(dm)\)
Thể tích chóp cụt đều bằng
\(\begin{array}{l}V = \frac{h}{3}\left( {{S_1} + {S_2} + \sqrt {{S_1}{S_2}} } \right)\\\,\,\,\,\, = \frac{{x\sqrt 6 }}{{3.3}}\left( {\frac{{{{(6 - 3x)}^2}\sqrt 3 }}{4}\, + \frac{{{{(6 - 2x)}^2}\sqrt 3 }}{4} + \frac{{(6 - 3x)(6 - 2x)\sqrt 3 }}{4}} \right)\\\,\,\,\,\, = \frac{{\sqrt {18} }}{{36}}\left( {19{x^3} - 90{x^2} + 108x} \right)\end{array}\)
Dùng casio xét trên khoảng \(\left( {0;2} \right)\), ta có \(\mathop {max}\limits_{\left( {0;2} \right)} V \approx 4,54\,(d{m^3})\).
Lời giải
Đáp án: 7,02.
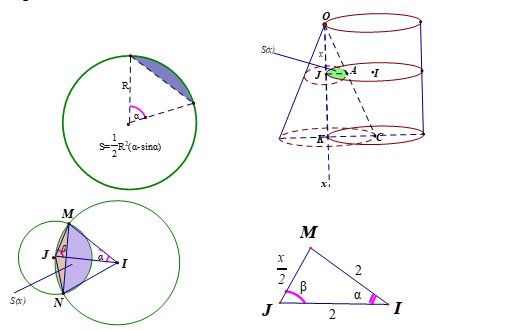
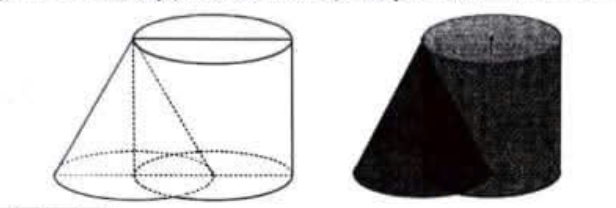
Gắn trục Ox như hình. Cắt khối giao của nón và trụ bởi 1 mặt phẳng vuông góc trục Ox tại x. Thiết diện là hình hợp bởi 2 hình viên phân của nón và trụ, có diện tích là S(x).
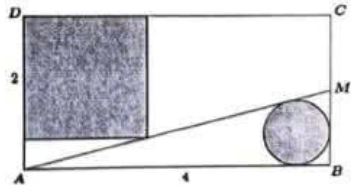
Xét tam giác OKC, có JA// KC, nên \[\frac{x}{4} = \frac{{JA}}{{KC}} = \frac{{JA}}{2} \Rightarrow JA = \frac{x}{2}\] là bán kính của đường tròn của hình nón tại vị trí x, tâm J. Đường tròn của hình trụ tại vị trí x có tâm I, bán kính bằng 2.
Gọi M là giao điểm của hai đường tròn tâm I và tâm J.
Giả sử \[\widehat {{\rm{MIJ}}} = \alpha \Rightarrow \widehat {{\rm{MIN}}} = 2\alpha ;\widehat {{\rm{MJI}}} = \beta \Rightarrow \widehat {{\rm{MJN}}} = 2\beta \].
Xét đường tròn tâm I, có \[IM = IN = JI = 2\]Xét đường tròn tâm J, có \[JM = JA = \frac{x}{2}\].
Áp đụng định lí cosin vào tam giác IJM, ta tính được:
\[cos\alpha = 1 - \frac{{{x^2}}}{{32}} \Rightarrow \alpha = {\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}});cos\beta = \frac{x}{8} \Rightarrow \beta = {\rm{ar}}cos\frac{x}{8}\]
Suy ra diện tích viên phân của đường tròn tâm I: \[{S_1} = 2(2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}) - \sin 2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}))\]
Diện tích viên phân của đường tròn tâm J: \[{S_2} = \frac{{{x^2}}}{8}(2{\rm{ar}}cos\frac{x}{8} - \sin 2{\rm{ar}}cos\frac{x}{8})\]
Nên diện tích thiết diện:
\[S(x) = {S_1} + {S_2} = 2(2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}) - \sin 2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}})) + \frac{{{x^2}}}{8}(2{\rm{ar}}cos\frac{x}{8} - \sin 2{\rm{ar}}cos\frac{x}{8})\]
Vậy thể tích phần giao của trụ và nón:
\[V = \int\limits_0^4 {S(x)dx = \int\limits_0^4 {(2(2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}}) - \sin 2{\rm{ar}}cos(1 - \frac{{{x^2}}}{{32}})) + \frac{{{x^2}}}{8}(2{\rm{ar}}cos\frac{x}{8} - \sin 2{\rm{ar}}cos\frac{x}{8}))dx} } = 7,02\]
(Theo Casio ta có kết quả trên)
Đáp số: 7,02.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.