Một lớp học gồm 40 học sinh trong đó có: 15 học sinh giỏi toán, 10 học sinh giỏi lý và 5 học sinh giỏi cả toán và lý. Chọn ngẫu nhiên một học sinh, xác suất để học sinh đó giỏi toán hoặc giỏi lý là:
Một lớp học gồm 40 học sinh trong đó có: 15 học sinh giỏi toán, 10 học sinh giỏi lý và 5 học sinh giỏi cả toán và lý. Chọn ngẫu nhiên một học sinh, xác suất để học sinh đó giỏi toán hoặc giỏi lý là:
A. \[\frac{3}{8}.\]
B. \[\frac{1}{2}.\]
C. \[\frac{1}{4}.\]
D. \[\frac{2}{3}.\]
Quảng cáo
Trả lời:
Giải bởi Vietjack
Gọi \[A\] là biến cố “học sinh giỏi toán”, \[B\] là biến cố “học sinh giỏi lý”.
Ta có \(AB\) là biến cố “học sinh giỏi toán và lý”.
\(A \cup B\) là biến cố “học sinh giỏi toán hoặc lý”.
Khi đó \(P\left( A \right) = \frac{{15}}{{40}} = \frac{3}{8}\,;\,\,P\left( B \right) = \frac{{10}}{{40}} = \frac{1}{4}\,;\,\,P\left( {AB} \right) = \frac{5}{{40}} = \frac{1}{8}.\)
Do đó \[P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{3}{8} + \frac{1}{4} - \frac{1}{8} = \frac{4}{8} = \frac{1}{2}.\] Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đổi đơn vị của enthalpy:
|
Chất |
\[{\Delta _{\rm{f}}}{\rm{H}}_{{\rm{298}}}^{\rm{o}}\] (kJ/g) |
\[{\Delta _{\rm{f}}}{\rm{H}}_{{\rm{298}}}^{\rm{o}}\] (kJ/mol) |
|
\[F{e_2}{O_3}\] |
−5,14 |
−822,4 |
|
\[A{l_2}{O_3}\] |
−16,37 |
−1669,74 |
Xét phản ứng: 2Al(s) + \[F{e_2}{O_3}\](s) \[A{l_2}{O_3}\](s) + 2Fe(s)
Biến thiên enthalpy của phản ứng:
\[{\Delta _r}H_{298}^o = {\Delta _f}H_{298}^0(A{l_2}{O_3}) + 2.{\Delta _f}H_{298}^0(Fe) - 2.{\Delta _f}H_{298}^0(Al) - {\Delta _f}H_{298}^0(F{e_2}{O_3})\]
= 1.( –1669,74) + 2.0 – 2.0 – 1.( –822,4) = –847,34 (kJ)
Nhiệt dung của sản phẩm: C = 102.0,84 + 2.56.0,67 = 160,72 (J.K-1).
Nhiệt độ tăng lên: \[\Delta T = \frac{{847,{{34.10}^3}.0,5}}{{160,72}} \approx 2636(K)\]
Nhiệt độ đạt được: (25 + 273) + 2636 = 2934 (K)
Chọn B.
Câu 2
A. \(45^\circ .\)
B. \(90^\circ .\)
C. \(30^\circ .\)
D. \(60^\circ .\)
Lời giải
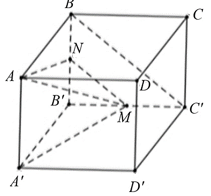
Giả sử cạnh của hình lập phương là \(a > 0.\)
Gọi \(N\) là trung điểm đoạn thẳng \(BB'.\)
Khi đó, \(MN\,{\rm{//}}\,BC'\) nên \(\left( {AM\,,\,\,BC'} \right) = \left( {AM\,,\,MN} \right)\).
Xét \(\Delta A'B'M\) vuông tại \(B'\), ta có
\(A'M = \sqrt {A'{{B'}^{\prime 2}} + B'{M^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2}.\)
Xét \(\Delta AA'M\) vuông tại \(A'\), ta có \(AM = \sqrt {A{{A'}^2} + A'{M^2}} = \sqrt {{a^2} + \frac{{5{a^2}}}{4}} = \frac{{3a}}{2}.\)
Có \[AN = A'M = \frac{{a\sqrt 5 }}{2}\,;\,\,MN = \frac{{BC'}}{2} = \frac{{a\sqrt 2 }}{2}.\]
Trong tam giác \[AMN\] ta có: \(\cos \widehat {AMN} = \frac{{M{A^2} + M{N^2} - A{N^2}}}{{2MA \cdot MN}} = \frac{{\frac{{9{a^2}}}{4} + \frac{{2{a^2}}}{4} - \frac{{5{a^2}}}{4}}}{{2 \cdot \frac{{3a}}{2} \cdot \frac{{a\sqrt 2 }}{2}}} = \frac{1}{{\sqrt 2 }}.\)
Suy ra \(\widehat {AMN} = 45^\circ .\) Vậy \[\left( {AM,\,\,BC'} \right) = \left( {AM,\,\,MN} \right) = \widehat {AMN} = 45^\circ .\] Chọn A.
Câu 3
A. \(30^\circ \).
B. \(45^\circ \).
C. \(60^\circ \).
D. \(90^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Việt Nam Cộng hòa.
B. Việt Nam Dân chủ Cộng hòa.
C. Cộng hòa Miền Nam Việt Nam.
D. Cộng hòa xã hội chủ nghĩa Việt Nam.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. for these children to expose their potential in these fields.
B. for these children exposing their potential in these fields.
C. that these children exposing their potential in these fields.
D. these children expose their potential in these fields.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập