Trong không gian Oxy, cho hai đường thẳng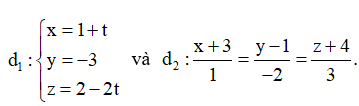 
Phương trình mặt phẳng (P) cách đều hai đường thẳng d1 và d2 có dạng ax+by +cz = 11. Giá trị của a+2b+3c bằng (nhập đáp án vào ô trống):
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đường thẳng \({d_1}\) có vectơ chỉ phương \[\overrightarrow u = \left( {1\,;\,\,0\,;\,\, - 2} \right)\] và đi qua điểm \(M\left( {1; - 3;2} \right).\)
Đường thẳng \({d_2}\) có vectơ chỉ phương \[\vec v = \left( {1\,;\,\, - 2\,;\,\,3} \right)\] và đi qua điểm \(N\left( { - 3\,;\,\,1\,;\,\, - 4} \right).\)
Ta có: \(\left[ {\vec v\,,\,\,\vec u} \right] = \left( {4\,;\,\,5\,;\,\,2} \right) \ne \vec 0\,;\,\,\overrightarrow {MN} = \left( { - 4\,;\,\,4\,;\,\, - 6} \right)\,;\,\,\left[ {\vec v\,,\,\,\vec u} \right] \cdot \overrightarrow {MN} = - 16 + 20 - 12 = - 8 \ne 0\)
\( \Rightarrow {d_1}\) và \({d_2}\) chéo nhau.
Mặt phẳng \(\left( P \right)\) cách đều hai đường thẳng \({d_1}\) và \({d_2}\) nên \(\left( P \right)\) nhận \(\left[ {\vec v\,,\,\,\vec u} \right] = \left( {4\,;\,\,5\,;\,\,2} \right)\) là vectơ pháp tuyến và đi qua trung điểm \(I\left( { - 1\,;\,\, - 1\,;\,\, - 1} \right)\) của đoạn MN.
Suy ra phương trình của \(\left( P \right):4\left( {x + 1} \right) + 5\left( {y + 1} \right) + 2\left( {z + 1} \right) = 0 \Leftrightarrow 4x + 5y + 2z + 11 = 0\)
\( \Rightarrow a = 4\,;\,\,b = 5\,;\,\,c = 2 \Rightarrow a + 2b + 3c = 20.\)
Đáp án cần nhập là: 20.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đổi đơn vị của enthalpy:
|
Chất |
\[{\Delta _{\rm{f}}}{\rm{H}}_{{\rm{298}}}^{\rm{o}}\] (kJ/g) |
\[{\Delta _{\rm{f}}}{\rm{H}}_{{\rm{298}}}^{\rm{o}}\] (kJ/mol) |
|
\[F{e_2}{O_3}\] |
−5,14 |
−822,4 |
|
\[A{l_2}{O_3}\] |
−16,37 |
−1669,74 |
Xét phản ứng: 2Al(s) + \[F{e_2}{O_3}\](s) \[A{l_2}{O_3}\](s) + 2Fe(s)
Biến thiên enthalpy của phản ứng:
\[{\Delta _r}H_{298}^o = {\Delta _f}H_{298}^0(A{l_2}{O_3}) + 2.{\Delta _f}H_{298}^0(Fe) - 2.{\Delta _f}H_{298}^0(Al) - {\Delta _f}H_{298}^0(F{e_2}{O_3})\]
= 1.( –1669,74) + 2.0 – 2.0 – 1.( –822,4) = –847,34 (kJ)
Nhiệt dung của sản phẩm: C = 102.0,84 + 2.56.0,67 = 160,72 (J.K-1).
Nhiệt độ tăng lên: \[\Delta T = \frac{{847,{{34.10}^3}.0,5}}{{160,72}} \approx 2636(K)\]
Nhiệt độ đạt được: (25 + 273) + 2636 = 2934 (K)
Chọn B.
Câu 2
A. \(45^\circ .\)
B. \(90^\circ .\)
C. \(30^\circ .\)
D. \(60^\circ .\)
Lời giải
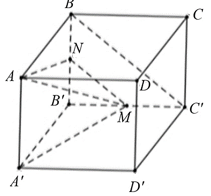
Giả sử cạnh của hình lập phương là \(a > 0.\)
Gọi \(N\) là trung điểm đoạn thẳng \(BB'.\)
Khi đó, \(MN\,{\rm{//}}\,BC'\) nên \(\left( {AM\,,\,\,BC'} \right) = \left( {AM\,,\,MN} \right)\).
Xét \(\Delta A'B'M\) vuông tại \(B'\), ta có
\(A'M = \sqrt {A'{{B'}^{\prime 2}} + B'{M^2}} = \sqrt {{a^2} + \frac{{{a^2}}}{4}} = \frac{{a\sqrt 5 }}{2}.\)
Xét \(\Delta AA'M\) vuông tại \(A'\), ta có \(AM = \sqrt {A{{A'}^2} + A'{M^2}} = \sqrt {{a^2} + \frac{{5{a^2}}}{4}} = \frac{{3a}}{2}.\)
Có \[AN = A'M = \frac{{a\sqrt 5 }}{2}\,;\,\,MN = \frac{{BC'}}{2} = \frac{{a\sqrt 2 }}{2}.\]
Trong tam giác \[AMN\] ta có: \(\cos \widehat {AMN} = \frac{{M{A^2} + M{N^2} - A{N^2}}}{{2MA \cdot MN}} = \frac{{\frac{{9{a^2}}}{4} + \frac{{2{a^2}}}{4} - \frac{{5{a^2}}}{4}}}{{2 \cdot \frac{{3a}}{2} \cdot \frac{{a\sqrt 2 }}{2}}} = \frac{1}{{\sqrt 2 }}.\)
Suy ra \(\widehat {AMN} = 45^\circ .\) Vậy \[\left( {AM,\,\,BC'} \right) = \left( {AM,\,\,MN} \right) = \widehat {AMN} = 45^\circ .\] Chọn A.
Câu 3
A. Việt Nam Cộng hòa.
B. Việt Nam Dân chủ Cộng hòa.
C. Cộng hòa Miền Nam Việt Nam.
D. Cộng hòa xã hội chủ nghĩa Việt Nam.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Cuộc đời của Mị tại nhà thống lí Pá Tra vô cùng vất vả, cực nhọc.
B. Cuộc sống tại nhà thống lí Pá Tra rút cạn sức sống của Mị, Mị chẳng màng đến cái chết.
C. Cuộc sống tại nhà thống lí Pá Tra vất vả, cực nhọc, rút cạn sức sống của Mị nhưng trong Mị vẫn còn khao khát, hi vọng vào cuộc sống.
D. Cuộc sống đầy khốn khó nhưng có hi vọng của Mị tại nhà thống lí Pá Tra.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Tự sự.
B. Miêu tả.
C. Nghị luận.
D. Hành chính công vụ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(30^\circ \).
B. \(45^\circ \).
C. \(60^\circ \).
D. \(90^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập