Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh \({\rm{AB}},{\rm{AC}}\) lần lượt là \({\rm{E}},{\rm{F}}\). Chứng minh rằng
Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh \({\rm{AB}},{\rm{AC}}\) lần lượt là \({\rm{E}},{\rm{F}}\). Chứng minh rằng
Quảng cáo
Trả lời:
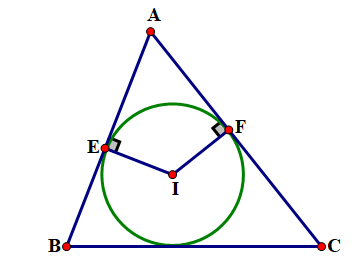
Ta có \({\rm{E}},{\rm{F}}\) lần lượt là hai tiếp điểm trên các cạnh AB và AC (gt)
Xét tứ giác AEIF có
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
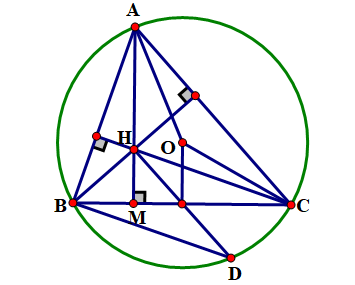
a) Xét tam giác ABD , ta có: \({\rm{OB}} = {\rm{OA}} = {\rm{OD}}( = {\rm{R}}){\rm{ hay OB}} = \frac{1}{2}{\rm{AD}}\)
Chứng tỏ vuông tại Bhay \({\rm{DB}} \bot {\rm{AB}}\) (đpcm)
Chứng minh tương tự ta có \({\rm{CD}} \bot {\rm{AC}}\).
b) Ta có \({\rm{BH}}//{\rm{DC}}\) (cùng vuông góc với AC ). Tương tự \({\rm{CH}}//{\rm{BD}}( \bot {\rm{AB}})\)
\( \Rightarrow \) Tứ giác BHCD là hình bình hành (các cạnh đối song song).
c) Ta có tam giác ACD vuông tại C (chứng minh trên) \( \Rightarrow {\rm{A}}{{\rm{C}}^2} + {\rm{D}}{{\rm{C}}^2} = {\rm{A}}{{\rm{D}}^2}\) (định lí Pythagore)
Mà \({\rm{DC}} = {\rm{BH}}({\rm{cmt}}) \Rightarrow {\rm{A}}{{\rm{C}}^2} + {\rm{B}}{{\rm{H}}^2} = {\rm{A}}{{\rm{D}}^2} = {(2{\rm{R}})^2} = 4{{\rm{R}}^2}\).
d) * Ta có M là trung điểm của BC (gt) mà tứ giác BHCD là hình bình hành (cmt) nên đường chéo thứ hai HD phải qua trung điểm M hay ba điểm \({\rm{H}},{\rm{M}},{\rm{D}}\) thẳng hàng.
* Xét tam giác AHD có O là trung điểm của AD (gt)
M là trung điểm của HD ( cmt ) nên OM là đường trung bình của tam giác \({\rm{AHD}} \Rightarrow {\rm{AH}} = 2{\rm{OM}}\).
Lời giải
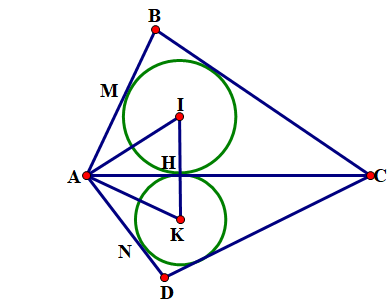
a) Đường tròn (I) tiếp xúc với cạnh AC tại điểm H (gt) \( \Rightarrow {\rm{IH}} \bot {\rm{AC}}\).
Tương tự đường tròn \(({\rm{K}})\) tiếp xúc với cạnh AC tại điểm \({\rm{H}} \Rightarrow {\rm{KH}} \bot {\rm{AC}}\).
\( \Rightarrow {\rm{Ba}}\) điểm \({\rm{I}},{\rm{H}},{\rm{K}}\) thẳng hàng.
b) Ta có đường tròn \(({\rm{I}})\) tiếp xúc với cạnh AB tại M hay AM là tiếp tuyến của đường tròn (I).
lại có AH là tiếp tuyến của đường tròn (I) (cmt)\( \Rightarrow {\rm{AM}} = {\rm{AH}}\) (*)(Tính chất hai tiếp tuyến cắt nhau)
Chứng minh tương tự, ta có \({\rm{AH}} = {\rm{AN}}\)(**)
Từ (*) và (**)\( \Rightarrow {\rm{AM}} = {\rm{AN}}\).
c) Ta có: \(\widehat {{\rm{IAK}}} = \widehat {{\rm{IAH}}} + \widehat {{\rm{HAK}}}\) mà \(\widehat {{\rm{IAH}}} = \frac{1}{2}\widehat {{\rm{MAH}}}\) (Tính chất hai tiếp tuyến cắt nhau)
\(\widehat {{\rm{HAK}}} = \frac{1}{2}\widehat {{\rm{HAN}}} \Rightarrow \widehat {{\rm{IAK}}}\)\( = \frac{1}{2}\widehat {{\rm{HAN}}} = \frac{1}{2}(\widehat {{\rm{MAH}}} + \widehat {{\rm{HAN}}})\)\( = \frac{1}{2}\widehat {{\rm{MAN}}}\)hay \( = \frac{1}{2}\widehat {{\rm{BAD}}}\)( đpcm)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.