Cho đường tròn \(\left( O \right)\) đường kính \(AB\). Dây cung \(MN\) vuông góc với \(AB\), (\(AM < BM\)). Hai đường thẳng \(BM\) và \(NA\) cắt nhau tại \(K\). Gọi \(H\) là chân đường vuông góc kẻ từ \(K\) đến đường thẳng \(AB\).
a) Chứng minh tứ giác \(AHKM\) nội tiếp trong một đường tròn.
b) Chứng minh rằng \(NB\;.\;HK = AN\;.\;HB\).
c) Chứng minh \(HM\) là tiếp tuyến của đường tròn \(\left( O \right)\).
Cho đường tròn \(\left( O \right)\) đường kính \(AB\). Dây cung \(MN\) vuông góc với \(AB\), (\(AM < BM\)). Hai đường thẳng \(BM\) và \(NA\) cắt nhau tại \(K\). Gọi \(H\) là chân đường vuông góc kẻ từ \(K\) đến đường thẳng \(AB\).
a) Chứng minh tứ giác \(AHKM\) nội tiếp trong một đường tròn.
b) Chứng minh rằng \(NB\;.\;HK = AN\;.\;HB\).
c) Chứng minh \(HM\) là tiếp tuyến của đường tròn \(\left( O \right)\).
Quảng cáo
Trả lời:

a) Chứng minh tứ giác \(AHKM\) nội tiếp trong một đường tròn.
+) Tứ giác \(AHKM\) có: \(\widehat {AHM} = 90^\circ \) (vì \(KH \bot AB\))
và \(\widehat {AMB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \widehat {AMK} = 90^\circ \) (kề bù với \(\widehat {AMB}\))
Suy ra tứ giác \(AHKM\) nội tiếp đường tròn đường kính \(AK\).
b) Chứng minh rằng: \(NB\;.\;HK = AN\;.\;HB\).
Xét \(\Delta ANB\) và \(\Delta KHB\) có:
+) \(\widehat {ANB} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow \widehat {ANB} = \widehat {KHB} = 90^\circ \);
+) Đường kính \(AB \bot MN \Rightarrow A\) là điểm chính giữa (quan hệ vuông góc giữa đường kính và dây) (hai góc nội tiếp chắn hai cung bằng nhau);
Suy ra
\( \Rightarrow \frac{{AN}}{{NB}} = \frac{{KH}}{{HB}}\)
\( \Rightarrow NB\;.\;HK = AN\;.\;HB\).
c) Chứng minh \(HM\) là tiếp tuyến của đường tròn \(\left( O \right)\).

+) Ta có \(HM\) giao với đường tròn \(\left( O \right)\) tại \(M\), ta phải chứng minh \(HM \bot OM\). Thật vậy:
Tứ giác \(AHKM\) nội tiếp \( \Rightarrow \widehat {HMK} = \widehat {HAK}\) (hai góc nội tiếp cùng chắn );
\(\widehat {HAK} = \widehat {NAB}\) (hai góc đối đỉnh);
\(\widehat {NAB} = \widehat {MAB}\) (\(AB \bot MN \Rightarrow B\) là điểm chính giữa , hai góc nội tiếp chắn hai cung bằng nhau);
\(\widehat {MAB} = \widehat {OMA}\) (\(\Delta OAM\) cân tại \(O\));
\( \Rightarrow \widehat {HMK} = \widehat {OMA}\left( { = \widehat {HAK} = \widehat {NAB} = \widehat {MAB}} \right) \Rightarrow \) \(\widehat {HMK} + \widehat {HMA} = \widehat {OMA} + \widehat {HMA}\);
Mà \(\widehat {HMK} + \widehat {HMA} = \widehat {AMK} = 90^\circ \) (kề bù với \(\widehat {AMB} = 90^\circ \), góc nội tiếp chắn nửa đường tròn);
\( \Rightarrow \widehat {OMA} + \widehat {HMA} = 90^\circ \Rightarrow \widehat {HMO} = 90^\circ \Rightarrow HM \bot OM\) tại \(M \in \left( O \right)\)
\( \Rightarrow HM\) là tiếp tuyến của \(\left( O \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
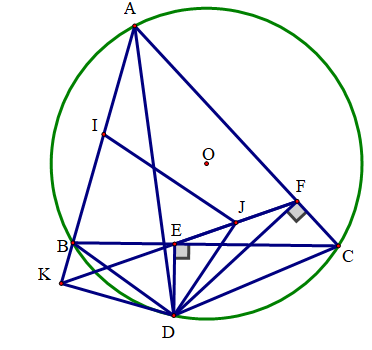
a) Chứng minh tứ giác CDEF và \(\widehat {DFE} = \widehat {DAB}\).
Xét tứ giác CDEF có:
+) \(\widehat {DEC} = {90^0}\) ( DE vuông góc với BC tại E)
+) \(\widehat {DFC} = {90^0}\) ( DF vuông góc với AC tại F)
\( \Rightarrow \)Tứ giác CDEF nội tiếp đường tròn đường kính DC (2 đỉnh E và F cùng nhìn cạnh DC dưới 1 góc vuông)
\( \Rightarrow \)
Mà trong đường tròn (O).
Do đó: \(\widehat {DFE} = \widehat {DAB}\) .
b) Chứng minh tứ giác DKBE nội tiếp và DB.DF = DA. DE.
Ta có: \(\widehat {KED} = \widehat {DCF}\) (góc ngoài bằng góc đối trong của tứ giác CDEF nội tiếp)
\(\widehat {DCF} = \widehat {DCA} = \widehat {KBD}\)( góc ngoài bằng góc đối trong đối với tứ giác ABDC nội tiếp đường tròn (O)).
Do đó: \(\widehat {KBD} = \widehat {KED} = \widehat {DCA}\) không đổi.
Suy ra tứ giác DKBE nội tiếp (2 đỉnh B, E cùng phía đối với cạnh KD và cùng nhìn cạnh KD dưới 1 góc không đổi)
Ta có:
Và trong đường tròn (O)
Suy ra \(\widehat {BDA} = \widehat {EDF}\).
Xét \(\Delta \)DBA và \(\Delta \)DEF có:
+) \(\widehat {DAB} = \widehat {DFE}\) (chứng minh trên)
+) \(\widehat {BDA} = \widehat {EDF}\) (chứng minh trên)
\(\Delta \)DBA \(\Delta \)DEF (góc - góc)
\( \Rightarrow \)\[\frac{{DB}}{{DE}} = \frac{{DA}}{{DF}} = \frac{{BA}}{{EF}}\] (*)
\( \Rightarrow \)DB.DF = DA.DE (điều phải chứng minh)
c) Gọi I, J lần lượt là trung điểm của AB và EF. Chứng minh IJ vuông góc với DJ.
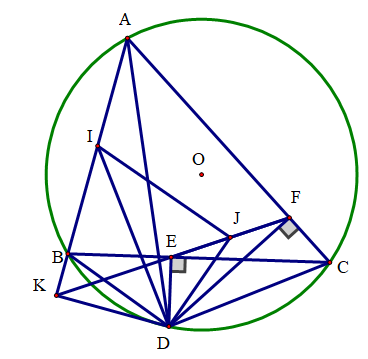
Từ (*) và I, J lần lượt là trung điểm của AB, EF nên ta có:
\[\frac{{DB}}{{DE}} = \frac{{BA}}{{EF}} = \frac{{2IB}}{{2JE}} = \frac{{IB}}{{JE}}\]
Xét \(\Delta \)DBI và \(\Delta \)DEJ ta có:
+)\(\widehat {DBI} = \widehat {DEJ}\) (\(\Delta \)DBA \(\Delta \)DEF chứng minh trên)
+) \[\frac{{DB}}{{DE}} = \frac{{IB}}{{JE}}\] ( chứng minh trên)
\( \Rightarrow \)\(\Delta \)DBI \(\Delta \)DEJ (cạnh – góc – cạnh)
\( \Rightarrow \)\(\widehat {DIB} = \widehat {DJE}\)\( \Rightarrow \)\(\widehat {KID} = \widehat {KJD}\) = góc không đổi.
\( \Rightarrow \)Tứ giác IKDJ nội tiếp (2 đỉnh I, J cùng phía với cạnh KD và cùng nhìn cạnh KD dưới 1 góc không đổi)
\( \Rightarrow \)\(\widehat {IKD} + \widehat {IJD} = {180^0}\).
Mà tứ giác DKBE nội tiếp nên \(\widehat {IKD} = \widehat {BKD} = {180^0} - \widehat {BED} = {90^0}\)
Do đó: \(\widehat {IJD}\) vuông hay IJ vuông góc với DJ.