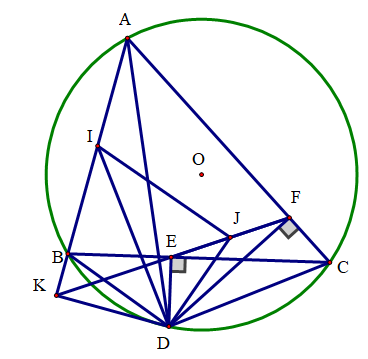
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O), (AB < AC). Gọi D là điểm trên cung nhỏ BC sao cho DB < DC. Từ D kẻ DE vuông góc với BC ( E thuộc BC), kẻ DF vuông góc với AC (F thuộc AC). Đường thẳng EF cắt tia AB tại K.

a) Chứng minh tứ giác CDEF và \(\widehat {DFE} = \widehat {DAB}\).

b) Chứng minh tứ giác DKBE nội tiếp và DB.DF = DA. DE.

c) Gọi I, J lần lượt là trung điểm của AB và EF. Chứng minh IJ vuông góc với DJ.

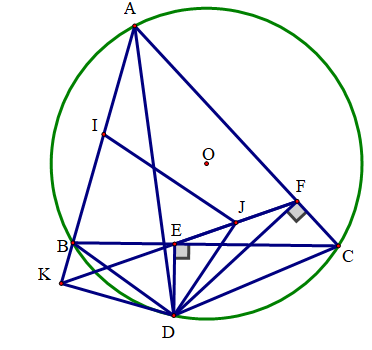
a) Chứng minh tứ giác CDEF và \(\widehat {DFE} = \widehat {DAB}\).

Xét tứ giác CDEF có:

+) \(\widehat {DEC} = {90^0}\) ( DE vuông góc với BC tại E)

+) \(\widehat {DFC} = {90^0}\) ( DF vuông góc với AC tại F)

\( \Rightarrow \)Tứ giác CDEF nội tiếp đường tròn đường kính DC (2 đỉnh E và F cùng nhìn cạnh DC dưới 1 góc vuông)

\( \Rightarrow \)

Mà  trong đường tròn (O).

Do đó: \(\widehat {DFE} = \widehat {DAB}\) .

b) Chứng minh tứ giác DKBE nội tiếp và DB.DF = DA. DE.

Ta có: \(\widehat {KED} = \widehat {DCF}\) (góc ngoài bằng góc đối trong của tứ giác CDEF nội tiếp)

\(\widehat {DCF} = \widehat {DCA} = \widehat {KBD}\)( góc ngoài bằng góc đối trong đối với tứ giác ABDC nội tiếp đường tròn (O)).

Do đó: \(\widehat {KBD} = \widehat {KED} = \widehat {DCA}\) không đổi.

Suy ra tứ giác DKBE nội tiếp (2 đỉnh B, E cùng phía đối với cạnh KD và cùng nhìn cạnh KD dưới 1 góc không đổi)

Ta có:

Và  trong đường tròn (O)

Suy ra \(\widehat {BDA} = \widehat {EDF}\).

Xét \(\Delta \)DBA  và \(\Delta \)DEF có:

+) \(\widehat {DAB} = \widehat {DFE}\) (chứng minh trên)

+) \(\widehat {BDA} = \widehat {EDF}\) (chứng minh trên)

\(\Delta \)DBA  \(\Delta \)DEF (góc - góc)

\( \Rightarrow \)\[\frac{{DB}}{{DE}} = \frac{{DA}}{{DF}} = \frac{{BA}}{{EF}}\] (*)

\( \Rightarrow \)DB.DF = DA.DE (điều phải chứng minh)

c) Gọi I, J lần lượt là trung điểm của AB và EF. Chứng minh IJ vuông góc với DJ.

Từ (*) và I, J lần lượt là trung điểm của AB, EF nên ta có:

     \[\frac{{DB}}{{DE}} = \frac{{BA}}{{EF}} = \frac{{2IB}}{{2JE}} = \frac{{IB}}{{JE}}\]

Xét \(\Delta \)DBI  và \(\Delta \)DEJ  ta có:

+)\(\widehat {DBI} = \widehat {DEJ}\) (\(\Delta \)DBA  \(\Delta \)DEF chứng minh trên)

+) \[\frac{{DB}}{{DE}} = \frac{{IB}}{{JE}}\] ( chứng minh trên)

\( \Rightarrow \)\(\Delta \)DBI  \(\Delta \)DEJ (cạnh – góc – cạnh)

\( \Rightarrow \)\(\widehat {DIB} = \widehat {DJE}\)\( \Rightarrow \)\(\widehat {KID} = \widehat {KJD}\) = góc không đổi.

\( \Rightarrow \)Tứ giác IKDJ nội tiếp (2 đỉnh I, J cùng phía với cạnh KD và cùng nhìn cạnh KD dưới 1 góc không đổi)

\( \Rightarrow \)\(\widehat {IKD} + \widehat {IJD} = {180^0}\).

Mà tứ giác DKBE nội tiếp nên \(\widehat {IKD} = \widehat {BKD} = {180^0} - \widehat {BED} = {90^0}\)

Do đó: \(\widehat {IJD}\) vuông hay IJ vuông góc với DJ.