Cho hàm số: \[y = \frac{3}{2}{x^2}\], \[y = - \frac{3}{2}{x^2}\]. Điền vào những ô trống của các bảng sau rồi vẽ hai đồ thị trên cùng một mặt phẳng tọa độ.
\[x\]
\[ - 2\]
\[ - 1\]
\[0\]
1
2
\[y = \frac{3}{2}{x^2}\]
\[x\]
\[ - 2\]
\[ - 1\]
\[0\]
1
2
\[y = - \frac{3}{2}{x^2}\]
Nhận xét về tính đối xứng của hai đồ thị đối với trục \[Ox\].
Cho hàm số: \[y = \frac{3}{2}{x^2}\], \[y = - \frac{3}{2}{x^2}\]. Điền vào những ô trống của các bảng sau rồi vẽ hai đồ thị trên cùng một mặt phẳng tọa độ.
|
\[x\] |
\[ - 2\] |
\[ - 1\] |
\[0\] |
1 |
2 |
|
\[y = \frac{3}{2}{x^2}\] |
|
|
|
|
|
|
\[x\] |
\[ - 2\] |
\[ - 1\] |
\[0\] |
1 |
2 |
|
\[y = - \frac{3}{2}{x^2}\] |
|
|
|
|
|
Nhận xét về tính đối xứng của hai đồ thị đối với trục \[Ox\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
Bảng giá trị của các hàm số
|
\[x\] |
\[ - 2\] |
\[ - 1\] |
\[0\] |
1 |
2 |
|
\[y = \frac{3}{2}{x^2}\] |
6 |
\[\frac{3}{2}\] |
0 |
\[\frac{3}{2}\] |
6 |
|
\[y = - \frac{3}{2}{x^2}\] |
\[ - 6\] |
\[ - \frac{3}{2}\] |
0 |
\[ - \frac{3}{2}\] |
\[ - 6\] |
Hai đồ thị trên đối xứng nhau qua trục \[Ox\].
![Cho hàm số: \[y = \frac{3}{2}{x^2}\], \[y = (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/2-1769563863.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Bảng giá trị của các hàm số:
|
\[x\] |
\[ - 2\] |
\[ - 1\] |
\[0\] |
1 |
2 |
|
\[y = \frac{1}{2}{x^2}\] |
2 |
\[ - \frac{1}{2}\] |
0 |
\[\frac{1}{2}\] |
2 |
|
\[y = {x^2}\] |
4 |
1 |
0 |
1 |
4 |
|
\[y = 2{x^2}\] |
8 |
2 |
0 |
2 |
8 |
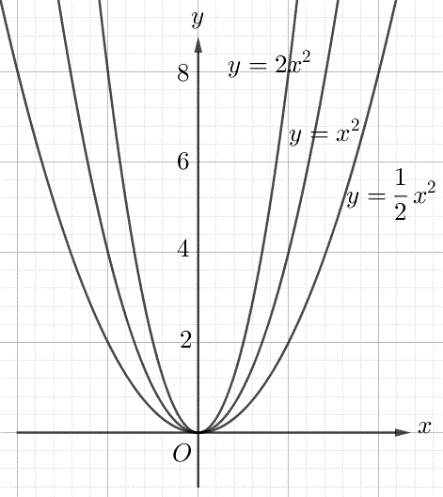
b) Ký hiệu \[{y_A}\] là tung độ của \[A\]. Thay \[x = - 1,5\]vào lần lượt các hàm số ta được:
\[{y_A} = \frac{1}{2}{\left( { - 1,5} \right)^2} = 1,125\]
\[{y_B} = {\left( { - 1,5} \right)^2} = 2,25\]
\[{y_C} = 2{\left( { - 1,5} \right)^2} = 4,5\]
c) Tương tự thay \[x = 1,5\] vào lần lượt các hàm số ta được:
\[{y_A} = \frac{1}{2}{\left( {1,5} \right)^2} = 1,125\]
\[{y_B} = {\left( {1,5} \right)^2} = 2,25\]
\[{y_C} = 2{\left( {1,5} \right)^2} = 4,5\]
Vậy \[A\] và \[A'\], \[B\] và \[B'\], \[C\] và \[C'\] đối xứng nhau qua \[Oy\].
d) Ta có \[y = \frac{1}{2}{x^2} \ge 0\]; \[y = {x^2} \ge 0\]; \[y = 2{x^2} \ge 0\] với mọi \[x\] nên với \[x = 0\] thì các hàm số đã cho đạt giá trị nhỏ nhất.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Bảng giá trị hàm số và đồ thị:
|
\[x\] |
\[ - 2\] |
\[ - 1\] |
\[0\] |
1 |
2 |
|
\[y = {x^2}\] |
4 |
1 |
0 |
1 |
4 |
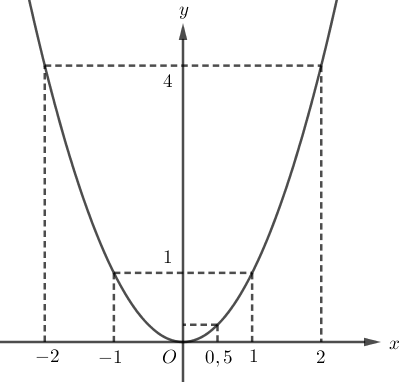
b) Tính các giá trị
|
\[x\] |
\[ - 8\] |
\[ - 1,3\] |
\[ - 0,75\] |
1,5 |
|
\[y = f\left( x \right) = {x^2}\] |
64 |
1,69 |
0,5625 |
2,25 |
c) d) học sinh tự làm.
Chẳng hạn để ước lượng giá trị \[{\left( {0,5} \right)^2}\] ta tìm tung độ \[{y_A}\] của điểm \[A\] thuộc đồ thị hàm số \[y = {x^2}\] ứng với hoành độ \[{x_A} = 0,5\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập