Sau những vụ va chạm giữa các xe trên đường, cảnh sát thường sử dụng công thức dưới đây để ước lượng tốc độ \(v\) (đơn vị: dặm/giờ) của xe từ vết trượt trên mặt đường sau khi thắng đột ngột \(d = \frac{1}{{30f}}{v^2}\). Trong đó, \(d\) là chiều dài vết trượt của bánh xe trên nền đường tính bằng feet \(({\rm{ft}}),f\) là hệ số ma sát giữa bánh xe và mặt đường (là thước đo sự "trơn trượt" của mặt đường).
Đường Cao tốc Long Thành - Dầu Giây có tốc độ giới hạn là \(100\;{\rm{km}}/{\rm{h}}\). Sau một vụ va chạm giữa hai xe, cảnh sát đo được vết trượt của một xe là \(d = 185{\rm{ft}}\) và hệ số ma sát mặt đường tại thời điểm đó là \(f = 0,73\). Chủ xe đó nói xe của ông không chạy quá tốc độ. Hãy áp dụng công thức trên để ước lượng tốc độ chiếc xe đó rồi cho biết lời nói của người chủ xe đúng hay sai? (Biết 1 dặm \( = 1609\;{\rm{m}})\). (Làm tròn các kết quả đến chữ số thập phân thứ hai).

Sau những vụ va chạm giữa các xe trên đường, cảnh sát thường sử dụng công thức dưới đây để ước lượng tốc độ \(v\) (đơn vị: dặm/giờ) của xe từ vết trượt trên mặt đường sau khi thắng đột ngột \(d = \frac{1}{{30f}}{v^2}\). Trong đó, \(d\) là chiều dài vết trượt của bánh xe trên nền đường tính bằng feet \(({\rm{ft}}),f\) là hệ số ma sát giữa bánh xe và mặt đường (là thước đo sự "trơn trượt" của mặt đường).
Đường Cao tốc Long Thành - Dầu Giây có tốc độ giới hạn là \(100\;{\rm{km}}/{\rm{h}}\). Sau một vụ va chạm giữa hai xe, cảnh sát đo được vết trượt của một xe là \(d = 185{\rm{ft}}\) và hệ số ma sát mặt đường tại thời điểm đó là \(f = 0,73\). Chủ xe đó nói xe của ông không chạy quá tốc độ. Hãy áp dụng công thức trên để ước lượng tốc độ chiếc xe đó rồi cho biết lời nói của người chủ xe đúng hay sai? (Biết 1 dặm \( = 1609\;{\rm{m}})\). (Làm tròn các kết quả đến chữ số thập phân thứ hai).

Quảng cáo
Trả lời:
1 dặm \( = 1609\;{\rm{m}} = 1,609\;{\rm{km}}\). Tốc độ của người lái xe là:
\(d = \frac{1}{{30f}} \cdot {v^2} \Rightarrow {v^2} = 30fd = 30 \cdot 185 \cdot 0,73 = 4051,5 \Rightarrow \left[ {\begin{array}{*{20}{l}}{v = 63,65{\rm{ (nh\^a n) }}}\\{v = - 63,65{\rm{ (loai) }}}\end{array}} \right.\)
\(v = 63,65 \cdot 1,609 = 102,41(\;{\rm{km}}/{\rm{h}})\)
Vì \(102,41 > 100\) (km/giờ) nên người chủ xe chạy quá tốc độ.
Vậy người chủ xe nói sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a)
- Bảng giá trị của \[y\] tương ứng với giá trị của \[x\] như sau:
|
\[x\] |
\[ - 2\] |
\[ - 1\] |
\[0\] |
\[1\] |
\[2\] |
|
\[y = {x^2}\] |
\[4\] |
\[1\] |
\[0\] |
\[1\] |
\[4\] |
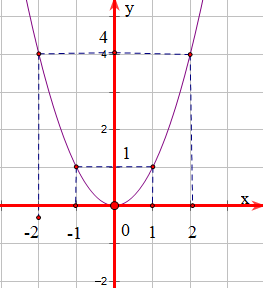
- Vẽ các điểm \[A\left( { - 2;4} \right),B\left( { - 1;1} \right),O\left( {0;0} \right),C\left( {1;1} \right),D\left( {2;4} \right)\] thuộc đồ thị hàm số \(y = {x^2}\) trong mặt phẳng \[Oxy\].
- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số \(y = {x^2}\)
b) Gọi \(C\) là điểm thuộc \(\left( P \right)\) có tung độ bằng 16.
Ta có: \({y_C} = 16 \Leftrightarrow {x^2}_C = 16 \Leftrightarrow {x_C} = \pm 4\). Vậy \(C\left( {4;16} \right)\) hoặc \(C\left( { - 4;16} \right)\).
c) Gọi \(D\) là điểm thuộc \(\left( P \right)\) cách đều hai trục tọa độ.
Ta có: \(d\left( {D,Ox} \right) = \left| {{y_D}} \right| = x_D^2;d\left( {D,Oy} \right) = \left| {{x_D}} \right|\).
Theo giả thiết ta có: \(x_D^2 = \left| {{x_D}} \right| \Leftrightarrow \left| {{x_D}} \right| = 0\) (loại) hoặc \(\left| {{x_D}} \right| = 1\).
Vậy \(D\left( {1;1} \right)\) hoặc \(D\left( { - 1;1} \right)\).
Lời giải
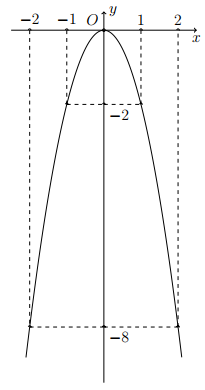
1. \((P)\) đi qua điểm \(A(1; - 2)\) khi và chỉ khi \( - 2 = a{.1^2} \Leftrightarrow a = - 2\).
2. Bảng giá trị

Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.