Cho tam giác \(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{G^2}}} \Rightarrow \frac{1}{{O{G^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{S{O^2}}} \Rightarrow OG = 2a\sqrt 3 \) vuông tại \(SO.OG = OH.SG \Rightarrow SG = \frac{{SO.OG}}{{SG}} = \frac{{6a.2a\sqrt 3 }}{{3a}} = 4a\sqrt 3 \), \( \Rightarrow DE = 8a\sqrt 3 \) và \(OD = \sqrt {O{G^2} + D{G^2}} = \sqrt {12{a^2} + 48{a^2}} = 2\sqrt {15} a\). Tính thể tích \(V = \frac{1}{3} \cdot \pi \cdot {\left( {2\sqrt {15} a} \right)^2} \cdot 6a = 120\pi {a^3}\) của hình nón nhận được khi quay tam giác \(\left( \alpha \right)\) quanh cạnh \({V_1}\).
Cho tam giác \(\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{G^2}}} \Rightarrow \frac{1}{{O{G^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{S{O^2}}} \Rightarrow OG = 2a\sqrt 3 \) vuông tại \(SO.OG = OH.SG \Rightarrow SG = \frac{{SO.OG}}{{SG}} = \frac{{6a.2a\sqrt 3 }}{{3a}} = 4a\sqrt 3 \), \( \Rightarrow DE = 8a\sqrt 3 \) và \(OD = \sqrt {O{G^2} + D{G^2}} = \sqrt {12{a^2} + 48{a^2}} = 2\sqrt {15} a\). Tính thể tích \(V = \frac{1}{3} \cdot \pi \cdot {\left( {2\sqrt {15} a} \right)^2} \cdot 6a = 120\pi {a^3}\) của hình nón nhận được khi quay tam giác \(\left( \alpha \right)\) quanh cạnh \({V_1}\).
Câu hỏi trong đề: 20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án !!
Quảng cáo
Trả lời:
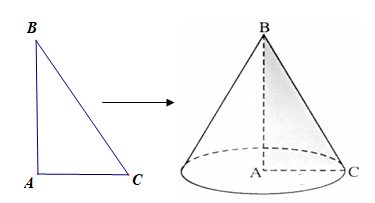
Khi quay tam giác \[R = HC = 2\] xung quanh trục \(AC\), ta thu được hình nón có bán kính đáy \(r = AB = a\), chiều cao \(h = AC\)và đường sinh là cạnh huyền \(l = BC\).
Xét tam giác \( = 2\sqrt 3 \) vuông tại \(V = \frac{1}{3}\pi {R^2}.AH\), ta có \(\frac{8}{{117}}\).
Vậy thể tích hình nón là : \(\frac{4}{{21}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
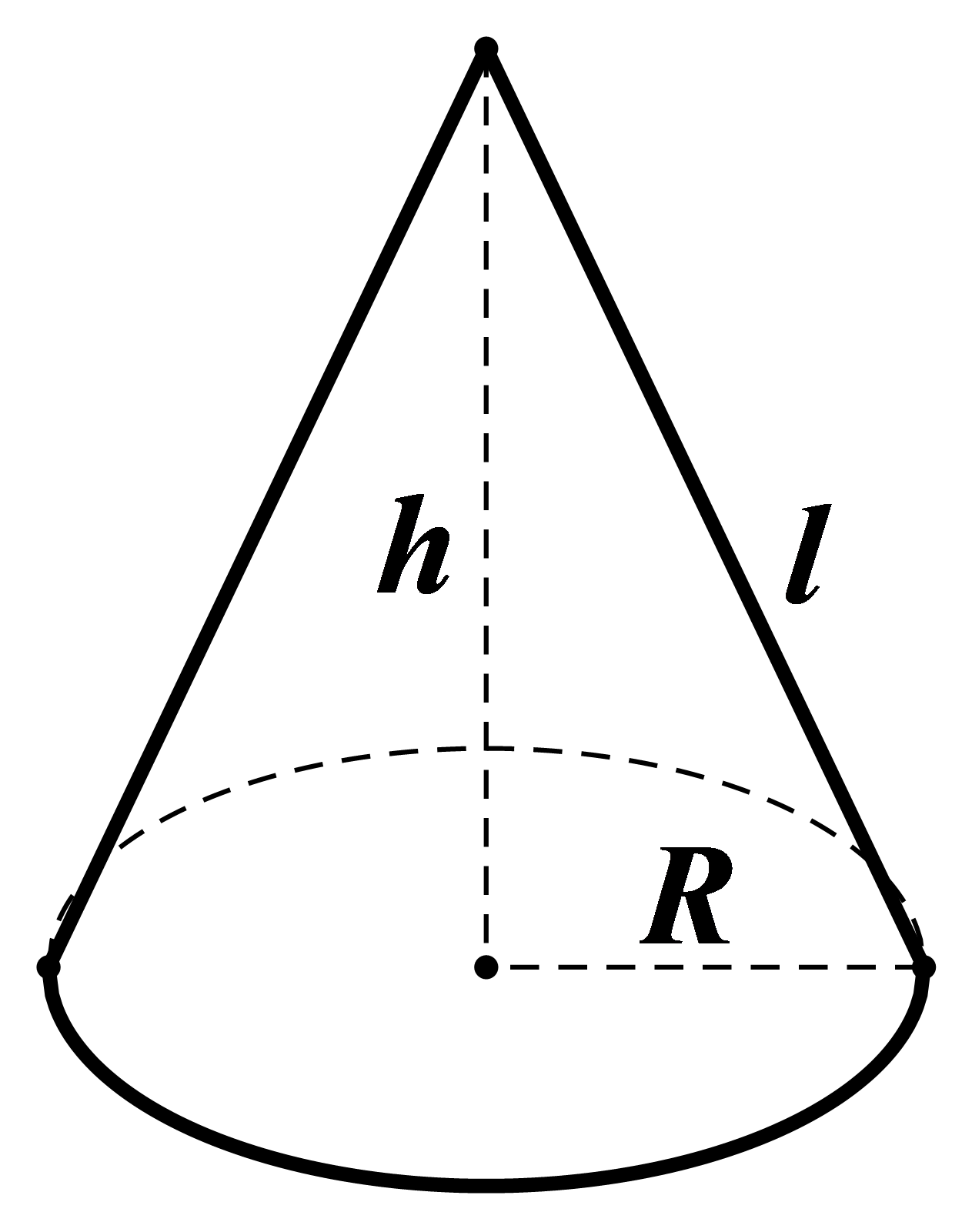
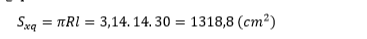
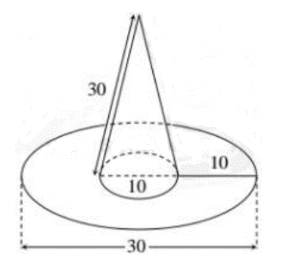
Vậy diện tích lá dùng để làm nón là 110%.1318,8=1450,68 cm2
Lời giải
Vì chiếc nón hình nón có đường sinh l = 30cm và bán kính đáy R = 40: 2 = 20cm nên diện tích xung quanh của chiếc nón là:
Sxq = pRl = p. 20. 30 = 600p (cm2)
diện tích là cần dùng cho một chiếc nón là: 2. 600p = 1200p cm2.
Vậy diện tích là cần dùng làm 5000 chiếc nón là: 500. 1200p = 600000p cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.