Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao \(h = 1,5\,{\rm{m}}\)gồm:
- Phần dưới có dạng hình trụ bán kính đáy \(R = 1\,{\rm{m}}\) và có chiều cao bằng \(\frac{1}{3}h\);
- Phần trên có dạng hình nón bán kính đáy bằng \(R\) đã bị cắt bỏ bớt một phần hình nón có bán kính đáy bằng \(\frac{1}{2}R\) ở phía trên (người ta thường gọi hình đó là hình nón cụt);
- Phần ở giữa rỗng có dạng hình trụ bán kính đáy bằng \(\frac{1}{4}R\) (tham khảo hình vẽ bên dưới).
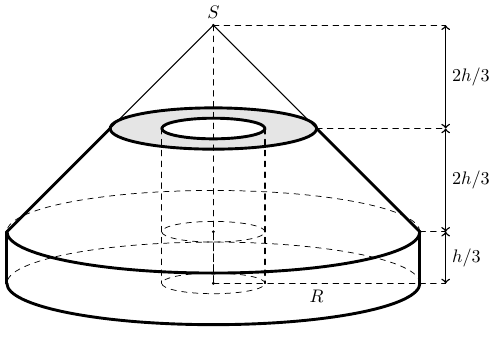
Tính thể tích của khối bê tông (làm tròn đến chữ số thập phân thứ ba).
Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao \(h = 1,5\,{\rm{m}}\)gồm:
- Phần dưới có dạng hình trụ bán kính đáy \(R = 1\,{\rm{m}}\) và có chiều cao bằng \(\frac{1}{3}h\);
- Phần trên có dạng hình nón bán kính đáy bằng \(R\) đã bị cắt bỏ bớt một phần hình nón có bán kính đáy bằng \(\frac{1}{2}R\) ở phía trên (người ta thường gọi hình đó là hình nón cụt);
- Phần ở giữa rỗng có dạng hình trụ bán kính đáy bằng \(\frac{1}{4}R\) (tham khảo hình vẽ bên dưới).

Tính thể tích của khối bê tông (làm tròn đến chữ số thập phân thứ ba).
Câu hỏi trong đề: 19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án !!
Quảng cáo
Trả lời:
Thể tích hình trụ bán kính đáy \(R\) và có chiều cao bằng \(\frac{h}{3}\):
\({V_1} = \pi {R^2}.\frac{h}{3} = \frac{1}{3}\pi {R^2}h\).
Thể tích hình nón cụt bán kính đáy lớn \(R\), bán kính đáy bé \(\frac{R}{2}\)và có chiều cao bằng \(\frac{{2h}}{3}\):
\({V_2} = \frac{1}{3}\pi {R^2}.\frac{{4h}}{3} - \frac{1}{3}\pi \frac{{{R^2}}}{4}.\frac{{2h}}{3} = \frac{7}{{18}}\pi {R^2}h\).
Thể tích hình trụ bán kính đáy \(\frac{R}{4}\) và có chiều cao bằng \(h\) (phần rỗng ở giữa):
\({V_3} = \pi \frac{{{R^2}}}{{16}}.h = \frac{1}{{16}}\pi {R^2}h\).
Thể tích của khối bê tông bằng:
\(V = {V_1} + {V_2} - {V_3}\) \( = \pi {R^2}h.\left( {\frac{1}{3} + \frac{7}{{18}} - \frac{1}{{16}}} \right)\)\( = \frac{{95}}{{144}}\pi {R^2}.h \approx 3,109\,{{\rm{m}}^3}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
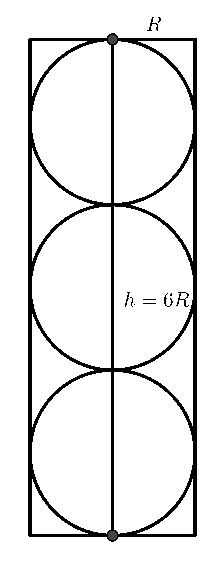
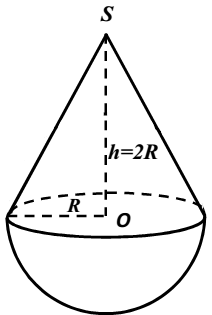
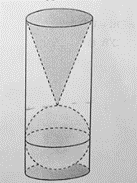
Đặt \(h,\,\,R\) lần lượt là đường cao và bán kính hình tròn đáy của hộp đựng bóng tennis.
Dễ thấy mỗi quả bóng tennis có cùng bán kính \(R\) với hình tròn đáy của hộp đựng bóng tennis và \(h = 6R\).
Do đó ta có:
Tổng thể tích của ba quả bóng là \({V_1} = 3.\frac{4}{3}\pi {R^3} = 4\pi {R^3}\);
Thể tích của hình trụ (hộp đựng bóng) là \({V_0} = \pi {R^2}h = 6\pi {R^3}\);
Thể tích phần còn trống của hộp đựng bóng là \({V_2} = {V_0} - {V_1} = 2\pi {R^3}\).
Khi đó tỉ lệ phần không gian còn trống so với hộp đựng bóng là \(\frac{{{V_2}}}{{{V_0}}} = \frac{1}{3} \approx 0,33\).
Suy ra \(a \approx 33\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.




![Người ta thả một viên bi có dạng hình cầu có bán kính \[2,7\,cm\] vào một chiếc cốc hình trụ đang chứa nước (tham khảo hình vẽ dưới). Biết rằng bán kính của phần trong đáy cốc bằng \[5,4\,cm\] và chiều cao của mực nước ban đầu trong cốc bằng \[4,5\,cm\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/16-1769749596.png)