Trong không gian với hệ tọa độ \(Oxyz\)(đơn vị trên mỗi trục là mét), tháp hải đăng Mũi Điện  - Phú Yên (là nơi đón ánh bình minh đầu tiên trên đất liền Tổ Quốc), chân tháp được đặt vuông góc với mặt đất (chiều từ chân tháp lên đỉnh tháp cùng hướng với chiều dương của trục \(Oz\)) ở vị trí điểm \(A\left( {12.040.271\,;\,1.418.620\,;\,84} \right)\).  Ngọn đèn của hải đăng được đặt trên đỉnh của tháp hải đăng hình trụ cao 26 m so với mặt đất và sử dụng pin năng lượng mặt trời, có thể phát tín hiệu ánh sáng xa khoảng 27 hải lý tương đương 50 km.

a) SAI

Các hệ số \(\left\{ \begin{array}{l} - 2a =  - 2\\ - 2b =  - 4\\ - 2c =  - 6\\d =  - 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c = 3\\d =  - 11\end{array} \right.\)

\( \Rightarrow \) Mặt cầu \((S)\) có tâm \(I\left( {1;2;3} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d}  = 5\).

b) ĐÚNG

Mặt phẳng \(\left( Q \right)\) tiếp xúc với mặt cầu \(\left( S \right)\) tại điểm \(A\left( {1;2;8} \right)\)

\( \Rightarrow \) \(\left( Q \right)\) có vtpt \(\overrightarrow n  = \left( {0;0;5} \right)\) và qua \(A\left( {1;2;8} \right)\)

\( \Rightarrow \) \(\left( Q \right):0.\left( {x - 1} \right) + 0.\left( {y - 2} \right) + 5\left( {z - 8} \right) = 0 \Leftrightarrow \left( Q \right):z = 8\).

c) ĐÚNG

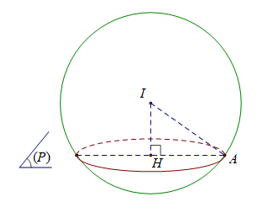
Do \(d\left[ {I,\left( P \right)} \right] = \frac{{\left| {1 + 2 + 3 - 3} \right|}}{{\sqrt {{1^2} + {1^2} + {1^2}} }} = \sqrt 3  < 5 = R\) nên \(\left( P \right)\) cắt mặt cầu \(\left( S \right)\) theo giao tuyến là đường tròn tâm \(H\), bán kính \(HA = \sqrt {{R^2} - {d^2}\left[ {I,(P)} \right]}  = \sqrt {{5^2} - {{\left( {\sqrt 3 } \right)}^2}}  = \sqrt {22} \)

d) SAI

Gọi \(\left( {{x_0},{y_0},{z_0}} \right)\) là một điểm nguyên nằm trên bề mặt của mặt cầu \(\left( S \right)\).

Ta có  \(x_0^2 + y_0^2 + z_0^2 - 2{x_0} - 4{y_0} - 6{z_0} - 11 = 0\)

\( \Leftrightarrow {\left( {{x_0} - 1} \right)^2} + {\left( {{y_0} - 2} \right)^2} + {\left( {{z_0} - 3} \right)^2} = 25\)

Đặt \(\left\{ \begin{array}{l}a = {x_0} - 1\\b = {y_0} - 2\\c = {z_0} - 3\end{array} \right.\) thì  \({a^2} + {b^2} + {c^2} = 25\) (*)  và \(a,b,c \in \mathbb{Z}\).

Số bộ \(\left( {a;b;c} \right)\) bằng với số bộ \(\left( {x;y;z} \right)\).

Do \({a^2},\,{b^2},{c^2}\) vai trò như nhau nên có thể giả sử \({a^2} \le {b^2} \le {c^2}\).

\({a^2} + {b^2} + {c^2} = 25 \Rightarrow 3{a^2} \le 25 \Rightarrow {a^2} \in \left\{ {0;1;4} \right\}\).

Với \({a^2} = 4\),

\(\left( * \right) \Rightarrow \) \({b^2} + {c^2} = 21\) à không có \(b,c\) nguyên.

 Với \({a^2} = 1\),

\(\left( * \right) \Rightarrow \) \({b^2} + {c^2} = 24 \Rightarrow \) không tồn tại \(b,c\) nguyên.

Với \({a^2} = 0\),

 \(\left( * \right) \Rightarrow \) \({b^2} + {c^2} = 25 = {3^2} + {4^2}\)

Chọn vị trí cho số \(0\)trong bộ \(\left( {a;b;c} \right)\) có \(3\)cách.

Chọn \(3\) hoặc \( - 3\) và xếp vào một vị trí trong bộ \(\left( {a;b;c} \right)\) có \(2.2 = 4\)cách.

Vị trí còn lại cho \(4\) hoặc \( - 4\) trong bộ \(\left( {a;b;c} \right)\) có \(2\)cách.

Vậy có \(3.4.2 = 24\) bộ \(\left( {a;b;c} \right)\).

Vậy có \(24\) bộ \(\left( {a;b;c} \right)\) hay \(24\) điểm nguyên nằm trên mặt cầu \(\left( S \right)\).