Ở cửa ra vào của nhà sách Nguyễn V\(0,1\% \)ăn Cừ có một thiết bị cảnh báo hàng hóa chưa được thanh toán khi qua cửa. Thiết bị phát chuông cảnh báo với \(99\% \) các hàng hóa ra cửa mà chưa thanh toán và  các hàng hóa đã thanh toán. Tỷ lệ hàng hóa qua cửa không được thanh toán là \(0,1\% \). Chọn ngẫu nhiên một hàng hóa khi đi qua cửa. Xét tính đúng sai của các mệnh đề sau?

Gọi \(A\) là biến cố “Hàng qua cửa đã được thanh toán” và \(B\) là biến cố “Thiết bị phát chuông cảnh báo”.

Tỷ lệ hàng qua cửa không được thanh toán là \(0,1\% \) tức là \(P\left( {\overline A } \right) = 0,1\% \) suy ra \(P\left( A \right) = 100\%  - 0,1\%  = 99,9\% \).

Ta có \(P\left( {B|A} \right) = 0,1\% \) và \(P\left( {B|\overline A } \right) = 99\% \);

\(P\left( {\overline B |A} \right) = 100\%  - P\left( {B|A} \right) = 99,9\% \); \(P\left( {\overline B |\overline A } \right) = 100\%  - P\left( {B|\overline A } \right) = 1\% \).

Ta có sơ đồ hình cây như sau:

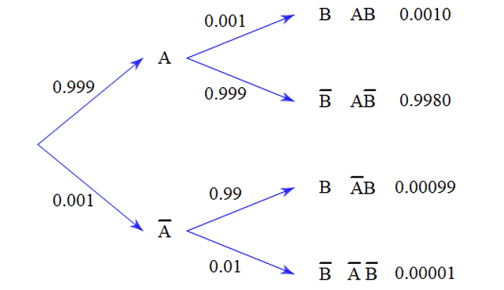
Từ đây ta có:

Xác suất để hàng qua cửa đã thanh toán là \(99,9\% \).

Xác suất để hàng qua cửa chưa thanh toán và thiết bị phát chuông cảnh báo là \(P\left( {\overline A B} \right) = 0,099\% \)

Xác suất để hàng hóa qua cửa đã thanh toán và thiết bị phát chuông cảnh báo là \(P\left( {\overline A B} \right) = 0,1\% \)