Cho tứ diện \(OABC\) với \(OBC\) là tam giác vuông tại \(O\), trong đó \(OB = 1\) và \(OC = \sqrt 3 \). Biết rằng \(OA\) vuông góc với mặt phẳng \(\left( {OBC} \right)\) và \(OA = \sqrt 3 \). Gọi \(M\) là trung điểm của \(BC\), tính khoảng cách giữa hai đường thẳng \(AB\) và \(OM\) (làm tròn kết quả đến hàng phần trăm).
Quảng cáo
Trả lời:
Đáp án:
Đáp số: 0,77.
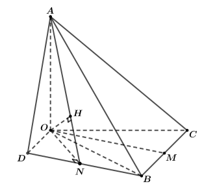
Qua điểm \(B\) kẻ đường thẳng \(d\parallel \,OM\), qua điểm \(O\) kẻ \(\Delta \parallel BC\). \(d \cap \Delta = \left\{ D \right\}\).
Khi đó \(OM\parallel DB\) hay \(OM\parallel \left( {ADB} \right)\).
Ta có \(d\left( {OM,AB} \right) = d\left( {OM,\left( {DAB} \right)} \right) = d\left( {O,\left( {DAB} \right)} \right)\).
Kẻ \(ON \bot DB\), \(OH \bot AN\).
Ta có \(\left\{ \begin{array}{l}DB \bot ON\\DB \bot OA\\OA,\,\,ON \subset \left( {AON} \right)\,\end{array} \right. \Rightarrow BD \bot \left( {AON} \right) \Rightarrow BD \bot OH\).
Ta có \(\left\{ \begin{array}{l}OH \bot AN\\OH \bot BD\\AN,\,\,BD \subset \left( {DAB} \right)\end{array} \right. \Rightarrow OH \bot \left( {DAB} \right)\) hay \(d\left( {O,\left( {DAB} \right)} \right) = OH\).
Tam giác \(OBC\) vuông tại \(O\) nên \(BC = \sqrt {O{B^2} + O{C^2}} = 2\).
Mặt khác, tam giác \(OBC\) vuông tại \(O\) có \(OM\) là trung tuyến ứng với cạnh huyền \(BC\) nên \(OM = \frac{1}{2}BC = 1\).
Tứ giác \(ODBM\) là hình bình hành nên \(\left\{ \begin{array}{l}OD = BM = \frac{1}{2}BC = 1\\OM = DB = 1\end{array} \right.\).
Ta có tam giác \(ODB\) có \(OD = OB = DB = 1\) nên tam giác \(ODB\) đều
Khi đó \[ON = \frac{{\sqrt 3 }}{2}\].
Xét tam giác \(AON\) vuông tại \(O\) có \(OH\) là đường cao:
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{N^2}}} \Rightarrow OH = \frac{{\sqrt {15} }}{5}\).
Vậy \(d\left( {OM,AB} \right) = d\left( {O,\left( {DAB} \right)} \right) = OH = \frac{{\sqrt {15} }}{5} \approx 0,77\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
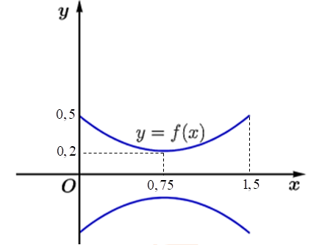
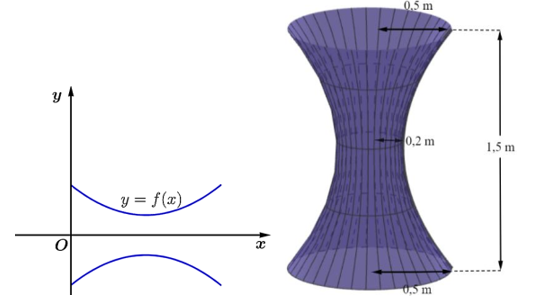
a) Gọi \(y = f\left( x \right)\)\( = a{x^2} + bx + c\).
Parabol cắt trục tung tại điểm \(\left( {0;0,5} \right)\) và đỉnh \(I\left( {0,75;0,2} \right)\)
Ta có hệ: \(\left\{ \begin{array}{l}c = 0,5\\a{\left( {0,75} \right)^2} + b.0,75 + c = 0,2\\ - \frac{b}{{2a}} = 0,75\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}c = \frac{1}{2}\\\frac{{9a}}{{16}} + \frac{{3b}}{4} + c = \frac{1}{5}\\3a + 2b = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{8}{{15}}\\b = - \frac{4}{5}\\c = \frac{1}{2}\end{array} \right.\).
Suy ra: \(f\left( x \right) = \frac{8}{{15}}{x^2} - \frac{4}{5}x + \frac{1}{2}\). Mệnh đề a) đúng.
b) Thể tích của chậu nước bằng
\(V = \pi \int\limits_0^{1,5} {{{\left[ {f\left( x \right)} \right]}^2}{\rm{d}}x} \)\( = \pi \int\limits_0^{1,5} {{{\left[ {\frac{8}{{15}}{x^2} - \frac{4}{5}x + \frac{1}{2}} \right]}^2}{\rm{d}}x} \)\( \approx 0,4618141201 \approx 0,5\). Mệnh đề b) đúng.
c) Tốc độ bơm nước vào bể \(5\) lít/phút \( = 5\,d{m^3}\)/phút \( = {5.10^{ - 3}}\,{m^3}\)/phút
Thể tích nước bơm sau \(1,5\) giờ \( = 1,5 \times 60 = 90\) phút là \({5.10^{ - 3}} \times 90 = 0,45 \approx 0,5\,\,{m^3}\). Mệnh đề c) đúng.
d) Gọi \(h\) là độ cao của nước trong chậu sau khi bơm được \(t\) phút.
Ta có: \({V_h} = \pi \int\limits_0^h {{{\left( {\frac{8}{{15}}{x^2} - \frac{4}{5}x + \frac{1}{2}} \right)}^2}{\rm{d}}x} \)\( = \pi \left( {\frac{{64}}{{1125}}{h^5} - \frac{{16}}{{75}}{h^4} + \frac{{88}}{{225}}{h^3} - \frac{2}{5}{h^2} + \frac{1}{4}h} \right)\) \({m^3}\).
Thể tích nước bơm sau \(t\) phút là \(V = 0,005t\,{m^3}\)
Khi đó: \(\pi \left( {\frac{{64}}{{1125}}{h^5} - \frac{{16}}{{75}}{h^4} + \frac{{88}}{{225}}{h^3} - \frac{2}{5}{h^2} + \frac{1}{4}h} \right) = 0,005t\) \(\left( * \right)\).
Tại thời điểm \(t = 20\) ta có: \(\pi \left( {\frac{{64}}{{1125}}{h^5} - \frac{{16}}{{75}}{h^4} + \frac{{88}}{{225}}{h^3} - \frac{2}{5}{h^2} + \frac{1}{4}h} \right) = 0,1\)\( \Rightarrow {h_0} \approx 0,1640803548\).
Đạo hàm theo biến \(t\) hai vế của \(\left( * \right)\) ta được:\(\left( {\frac{{64}}{{225}}{h^4} - \frac{{64}}{{75}}{h^3} + \frac{{264}}{{225}}{h^2} - \frac{4}{5}h + \frac{1}{4}} \right)h'\left( t \right) = \frac{{0,005}}{\pi }\)
Tốc độ dâng lên của nước
\(v\left( t \right) = h'\left( t \right) = \frac{{0,005}}{{\pi \left( {\frac{{64}}{{225}}{h^4} - \frac{{64}}{{75}}{h^3} + \frac{{264}}{{225}}{h^2} - \frac{4}{5}h + \frac{1}{4}} \right)}}\)
Tại thời điểm \(t = 20\),\({h_0} \approx 0,1640803548\) tốc độ dâng của nước là:
\(v\left( {20} \right) = h'\left( {20} \right) = \frac{{0,005}}{{\pi \left( {\frac{{64}}{{225}}h_0^4 - \frac{{64}}{{75}}h_0^3 + \frac{{264}}{{225}}h_0^2 - \frac{4}{5}{h_0} + \frac{1}{4}} \right)}}\)
\( \approx 0,01084447993\)m/phút.\( \approx 0,01\). Mệnh đề d) đúng.Lời giải
Đáp án: 80.
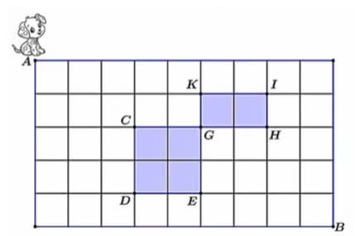
Ta có: \(A = (0;0;0)\) và \(B = (0;600;0)\).
Độ dài quãng đường \(AB\) là \(AB = \sqrt {{{(0 - 0)}^2} + {{(600 - 0)}^2} + {{(0 - 0)}^2}} = \sqrt {{0^2} + {{600}^2} + {0^2}} = 600\) (m).
Thời gian đi từ \(A\) đến \(B\) là 6 phút.
Tốc độ của xe mô tô khi đi từ \(A\) đến \(B\) là: \(v = \frac{{AB}}{6} = \frac{{600}}{6} = 100\) (m/phút).
Sau khi đổi hướng tại \(B\), xe đi từ \(B(0;600;0)\) đến \(C(1500;600;0)\) với tốc độ không đổi \(v = 100\) m/phút.
Giả sử tại thời điểm \(t\) (phút) kể từ khi đổi hướng tại \(B\), xe đang ở vị trí \(M(x;y;z)\).
Vecto chỉ phương của đoạn \(BC\) là: \({\vec u_{BC}} = \frac{{\overrightarrow {BC} }}{{|\overrightarrow {BC} |}} = \frac{{(1500 - 0;600 - 600;0 - 0)}}{{\sqrt {{{1500}^2} + {0^2} + {0^2}} }} = \frac{{(1500;0;0)}}{{1500}} = (1;0;0)\).
Vị trí của xe tại thời điểm \(t\) là: \(M(t) = B + v \cdot t \cdot {\vec u_{BC}}\)
\(M(t) = (0;600;0) + 100 \cdot t \cdot (1;0;0)\)
\(M(t) = (0 + 100t;600 + 0;0 + 0)\)
\(M(t) = (100t;600;0)\).
Khoảng cách từ xe mô tô đến vị trí xuất phát \(A(0;0;0)\) tại thời điểm \(t\) là \(D(t)\):
\(D(t) = |\overrightarrow {AM(t)} | = \sqrt {{{(100t - 0)}^2} + {{(600 - 0)}^2} + {{(0 - 0)}^2}} \)\( = \sqrt {{{(100t)}^2} + {{600}^2}} \)\( = 100\sqrt {{t^2} + 36} \).
Tốc độ thay đổi khoảng cách của xe mô tô đối với vị trí xuất phát \(A\) chính là đạo hàm của \(D\left( t \right)\) theo \(t\):
\(D'\left( t \right) = {\left( {100\sqrt {{t^2} + 36} } \right)^\prime }\)\( = 100 \cdot \frac{1}{{2\sqrt {{t^2} + 36} }} \cdot (2t)\)\( = \frac{{100t}}{{\sqrt {{t^2} + 36} }}\).
Tại phút thứ 8 kể từ khi xe đổi hướng, tức là \(t = 8\) phút.
Thay \(t = 8\) vào biểu thức \(D'\left( t \right)\) ta được:
\(D'\left( 8 \right) = \frac{{100 \cdot 8}}{{\sqrt {{8^2} + 36} }}\)\( = \frac{{800}}{{\sqrt {64 + 36} }}\)\( = \frac{{800}}{{\sqrt {100} }}\)\( = \frac{{800}}{{10}}\)\( = 80\) (m/phút).
Vậy, ở phút thứ 8 kể từ khi xe đổi hướng, tốc độ thay đổi khoảng cách của xe mô tô đối với vị trí xuất phát \(A\) là 80 m/phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.