Một loại gạch men có kích thước hình vuông \(60 \times 60{\rm{ cm}}\). Người ta thiết kế hoa văn cho viên gạch bằng cách tạo đường tròn \(\left( {{C_1}} \right)\) nội tiếp hình vuông ban đầu, phần nằm ngoài đường tròn \(\left( {{C_1}} \right)\) mà thuộc viên gạch thì được tô màu đậm. Tiếp theo họ tạo ra một hình vuông nội tiếp đường tròn \(\left( {{C_1}} \right)\), bên trong hình vuông này lại có một đường tròn nội tiếp \(\left( {{C_2}} \right)\); và họ tiếp tục tô màu đậm cho phần nằm ngoài đường tròn \(\left( {{C_2}} \right)\) mà thuộc hình vuông này. Quy luật này cứ tiếp tục vô hạn lần (tham khảo hình vẽ).
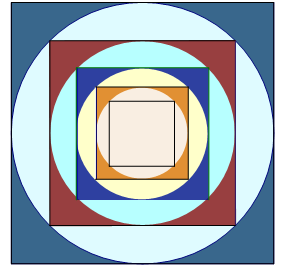
Hỏi tổng diện tích thuộc về viên gạch được tô màu đậm là bao nhiêu cm vuông? Kết quả được làm tròn đến hàng đơn vị của cm vuông.
Một loại gạch men có kích thước hình vuông \(60 \times 60{\rm{ cm}}\). Người ta thiết kế hoa văn cho viên gạch bằng cách tạo đường tròn \(\left( {{C_1}} \right)\) nội tiếp hình vuông ban đầu, phần nằm ngoài đường tròn \(\left( {{C_1}} \right)\) mà thuộc viên gạch thì được tô màu đậm. Tiếp theo họ tạo ra một hình vuông nội tiếp đường tròn \(\left( {{C_1}} \right)\), bên trong hình vuông này lại có một đường tròn nội tiếp \(\left( {{C_2}} \right)\); và họ tiếp tục tô màu đậm cho phần nằm ngoài đường tròn \(\left( {{C_2}} \right)\) mà thuộc hình vuông này. Quy luật này cứ tiếp tục vô hạn lần (tham khảo hình vẽ).

Hỏi tổng diện tích thuộc về viên gạch được tô màu đậm là bao nhiêu cm vuông? Kết quả được làm tròn đến hàng đơn vị của cm vuông.
Quảng cáo
Trả lời:
Đáp án:
Đáp án: \(1545\).
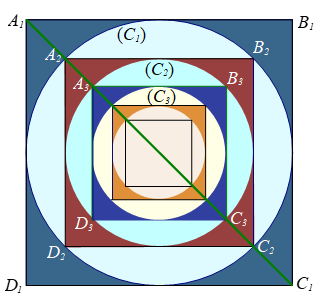
Đặt \({A_1}{B_1} = a\), ta có:
* Diện tích hình vuông \({A_1}{B_1}{C_1}{D_1}\) là \({S_{V1}} = {a^2}\).
Bán kính hình tròn \(\left( {{C_1}} \right)\) là \({R_1} = \frac{{{A_1}{B_1}}}{2} = \frac{a}{2}\) Þ Diện tích hình tròn \(\left( {{C_1}} \right)\) là \({S_{T1}} = \pi .{\left( {\frac{a}{2}} \right)^2} = \frac{{\pi {a^2}}}{4}\).
* Hình vuông \({A_2}{B_2}{C_2}{D_2}\) có đường chéo \({A_2}{C_2} = 2{R_1} = a\) Þ Cạnh \({A_2}{B_2} = \frac{{{A_2}{C_2}}}{{\sqrt 2 }} = \frac{a}{{\sqrt 2 }}\)
Þ Diện tích hình vuông \({A_2}{B_2}{C_2}{D_2}\) là \({S_{V2}} = {\left( {\frac{a}{{\sqrt 2 }}} \right)^2} = \frac{{{a^2}}}{2}\).
Bán kính hình tròn \(\left( {{C_2}} \right)\) là \({R_2} = \frac{{{A_2}{B_2}}}{2} = \frac{a}{{2\sqrt 2 }}\)
Þ Diện tích hình tròn \(\left( {{C_2}} \right)\) là \({S_{T2}} = \pi .{\left( {\frac{a}{{2\sqrt 2 }}} \right)^2} = \frac{{\pi {a^2}}}{8}\).
* Hình vuông \({A_3}{B_3}{C_3}{D_3}\) có đường chéo \({A_3}{C_3} = 2{R_2} = \frac{a}{{\sqrt 2 }}\) Þ Cạnh \({A_3}{B_3} = \frac{a}{{\sqrt 2 .\sqrt 2 }} = \frac{a}{2}\)
Þ Diện tích hình vuông \({A_3}{B_3}{C_3}{D_3}\) là \({S_{V3}} = {\left( {\frac{a}{2}} \right)^2} = \frac{{{a^2}}}{4}\)
Bán kính hình tròn \(\left( {{C_3}} \right)\) là \({R_3} = \frac{1}{2}{A_3}{B_3} = \frac{a}{4}\)
Þ Diện tích hình tròn \(\left( {{C_3}} \right)\) là \[{S_{T3}} = \pi .{\left( {\frac{a}{4}} \right)^2} = \frac{{\pi {a^2}}}{{16}}\].
* Tiếp tục theo quy luật trên, ta có:
Diện tích các hình vuông \({A_1}{B_1}{C_1}{D_1},{A_2}{B_2}{C_2}{D_2},{A_3}{B_3}{C_3}{D_3},...\) lần lượt là \({a^2},\frac{{{a^2}}}{2},\frac{{{a^2}}}{4},...\) lập thành cấp số nhân lùi vô hạn với số hạng đầu \({S_{V1}} = {a^2}\), công bội \({q_1} = \frac{1}{2}\).
Þ Tổng diện tích các hình vuông là \({S_V} = {a^2} + \frac{{{a^2}}}{2} + \frac{{{a^2}}}{4} + ... = \frac{{{a^2}}}{{1 - \frac{1}{2}}} = 2{a^2}\)
Diện tích các hình tròn nội tiếp tương ứng lần lượt là \(\frac{{\pi {a^2}}}{4},\frac{{\pi {a^2}}}{8},\frac{{\pi {a^2}}}{{16}},...\)lập thành cấp số nhân lùi vô hạn với số hạng đầu \({S_{T1}} = \frac{{\pi {a^2}}}{4}\), công bội \({q_2} = \frac{1}{2}\).
Þ Tổng diện các hình tròn tương ứng là \({S_T} = \frac{{\pi {a^2}}}{4} + \frac{{\pi {a^2}}}{8} + \frac{{\pi {a^2}}}{{16}} + ... = \frac{{\frac{{\pi {a^2}}}{4}}}{{1 - \frac{1}{2}}} = \frac{{\pi {a^2}}}{2}\)
Þ Tổng diện tích phần tô màu đậm là: \(S = {S_V} - {S_T} = 2{a^2} - \frac{{\pi {a^2}}}{2} = \frac{{{a^2}\left( {4 - \pi } \right)}}{2}\left( {c{m^2}} \right)\)
Với \(a = 60\left( {cm} \right)\), ta có tổng diện tích phần tô màu đậm là: \(S = \frac{{{{60}^2}.\left( {4 - \pi } \right)}}{2} \approx 1545\left( {c{m^2}} \right)\)Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
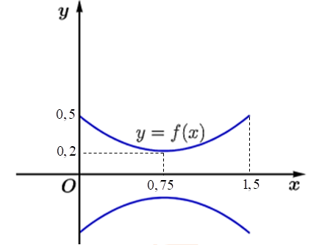
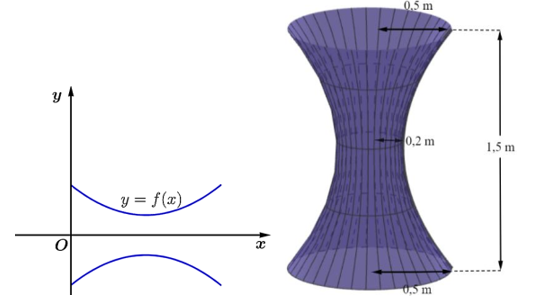
a) Gọi \(y = f\left( x \right)\)\( = a{x^2} + bx + c\).
Parabol cắt trục tung tại điểm \(\left( {0;0,5} \right)\) và đỉnh \(I\left( {0,75;0,2} \right)\)
Ta có hệ: \(\left\{ \begin{array}{l}c = 0,5\\a{\left( {0,75} \right)^2} + b.0,75 + c = 0,2\\ - \frac{b}{{2a}} = 0,75\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}c = \frac{1}{2}\\\frac{{9a}}{{16}} + \frac{{3b}}{4} + c = \frac{1}{5}\\3a + 2b = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{8}{{15}}\\b = - \frac{4}{5}\\c = \frac{1}{2}\end{array} \right.\).
Suy ra: \(f\left( x \right) = \frac{8}{{15}}{x^2} - \frac{4}{5}x + \frac{1}{2}\). Mệnh đề a) đúng.
b) Thể tích của chậu nước bằng
\(V = \pi \int\limits_0^{1,5} {{{\left[ {f\left( x \right)} \right]}^2}{\rm{d}}x} \)\( = \pi \int\limits_0^{1,5} {{{\left[ {\frac{8}{{15}}{x^2} - \frac{4}{5}x + \frac{1}{2}} \right]}^2}{\rm{d}}x} \)\( \approx 0,4618141201 \approx 0,5\). Mệnh đề b) đúng.
c) Tốc độ bơm nước vào bể \(5\) lít/phút \( = 5\,d{m^3}\)/phút \( = {5.10^{ - 3}}\,{m^3}\)/phút
Thể tích nước bơm sau \(1,5\) giờ \( = 1,5 \times 60 = 90\) phút là \({5.10^{ - 3}} \times 90 = 0,45 \approx 0,5\,\,{m^3}\). Mệnh đề c) đúng.
d) Gọi \(h\) là độ cao của nước trong chậu sau khi bơm được \(t\) phút.
Ta có: \({V_h} = \pi \int\limits_0^h {{{\left( {\frac{8}{{15}}{x^2} - \frac{4}{5}x + \frac{1}{2}} \right)}^2}{\rm{d}}x} \)\( = \pi \left( {\frac{{64}}{{1125}}{h^5} - \frac{{16}}{{75}}{h^4} + \frac{{88}}{{225}}{h^3} - \frac{2}{5}{h^2} + \frac{1}{4}h} \right)\) \({m^3}\).
Thể tích nước bơm sau \(t\) phút là \(V = 0,005t\,{m^3}\)
Khi đó: \(\pi \left( {\frac{{64}}{{1125}}{h^5} - \frac{{16}}{{75}}{h^4} + \frac{{88}}{{225}}{h^3} - \frac{2}{5}{h^2} + \frac{1}{4}h} \right) = 0,005t\) \(\left( * \right)\).
Tại thời điểm \(t = 20\) ta có: \(\pi \left( {\frac{{64}}{{1125}}{h^5} - \frac{{16}}{{75}}{h^4} + \frac{{88}}{{225}}{h^3} - \frac{2}{5}{h^2} + \frac{1}{4}h} \right) = 0,1\)\( \Rightarrow {h_0} \approx 0,1640803548\).
Đạo hàm theo biến \(t\) hai vế của \(\left( * \right)\) ta được:\(\left( {\frac{{64}}{{225}}{h^4} - \frac{{64}}{{75}}{h^3} + \frac{{264}}{{225}}{h^2} - \frac{4}{5}h + \frac{1}{4}} \right)h'\left( t \right) = \frac{{0,005}}{\pi }\)
Tốc độ dâng lên của nước
\(v\left( t \right) = h'\left( t \right) = \frac{{0,005}}{{\pi \left( {\frac{{64}}{{225}}{h^4} - \frac{{64}}{{75}}{h^3} + \frac{{264}}{{225}}{h^2} - \frac{4}{5}h + \frac{1}{4}} \right)}}\)
Tại thời điểm \(t = 20\),\({h_0} \approx 0,1640803548\) tốc độ dâng của nước là:
\(v\left( {20} \right) = h'\left( {20} \right) = \frac{{0,005}}{{\pi \left( {\frac{{64}}{{225}}h_0^4 - \frac{{64}}{{75}}h_0^3 + \frac{{264}}{{225}}h_0^2 - \frac{4}{5}{h_0} + \frac{1}{4}} \right)}}\)
\( \approx 0,01084447993\)m/phút.\( \approx 0,01\). Mệnh đề d) đúng.Lời giải
Đáp án: 80.
Ta có: \(A = (0;0;0)\) và \(B = (0;600;0)\).
Độ dài quãng đường \(AB\) là \(AB = \sqrt {{{(0 - 0)}^2} + {{(600 - 0)}^2} + {{(0 - 0)}^2}} = \sqrt {{0^2} + {{600}^2} + {0^2}} = 600\) (m).
Thời gian đi từ \(A\) đến \(B\) là 6 phút.
Tốc độ của xe mô tô khi đi từ \(A\) đến \(B\) là: \(v = \frac{{AB}}{6} = \frac{{600}}{6} = 100\) (m/phút).
Sau khi đổi hướng tại \(B\), xe đi từ \(B(0;600;0)\) đến \(C(1500;600;0)\) với tốc độ không đổi \(v = 100\) m/phút.
Giả sử tại thời điểm \(t\) (phút) kể từ khi đổi hướng tại \(B\), xe đang ở vị trí \(M(x;y;z)\).
Vecto chỉ phương của đoạn \(BC\) là: \({\vec u_{BC}} = \frac{{\overrightarrow {BC} }}{{|\overrightarrow {BC} |}} = \frac{{(1500 - 0;600 - 600;0 - 0)}}{{\sqrt {{{1500}^2} + {0^2} + {0^2}} }} = \frac{{(1500;0;0)}}{{1500}} = (1;0;0)\).
Vị trí của xe tại thời điểm \(t\) là: \(M(t) = B + v \cdot t \cdot {\vec u_{BC}}\)
\(M(t) = (0;600;0) + 100 \cdot t \cdot (1;0;0)\)
\(M(t) = (0 + 100t;600 + 0;0 + 0)\)
\(M(t) = (100t;600;0)\).
Khoảng cách từ xe mô tô đến vị trí xuất phát \(A(0;0;0)\) tại thời điểm \(t\) là \(D(t)\):
\(D(t) = |\overrightarrow {AM(t)} | = \sqrt {{{(100t - 0)}^2} + {{(600 - 0)}^2} + {{(0 - 0)}^2}} \)\( = \sqrt {{{(100t)}^2} + {{600}^2}} \)\( = 100\sqrt {{t^2} + 36} \).
Tốc độ thay đổi khoảng cách của xe mô tô đối với vị trí xuất phát \(A\) chính là đạo hàm của \(D\left( t \right)\) theo \(t\):
\(D'\left( t \right) = {\left( {100\sqrt {{t^2} + 36} } \right)^\prime }\)\( = 100 \cdot \frac{1}{{2\sqrt {{t^2} + 36} }} \cdot (2t)\)\( = \frac{{100t}}{{\sqrt {{t^2} + 36} }}\).
Tại phút thứ 8 kể từ khi xe đổi hướng, tức là \(t = 8\) phút.
Thay \(t = 8\) vào biểu thức \(D'\left( t \right)\) ta được:
\(D'\left( 8 \right) = \frac{{100 \cdot 8}}{{\sqrt {{8^2} + 36} }}\)\( = \frac{{800}}{{\sqrt {64 + 36} }}\)\( = \frac{{800}}{{\sqrt {100} }}\)\( = \frac{{800}}{{10}}\)\( = 80\) (m/phút).
Vậy, ở phút thứ 8 kể từ khi xe đổi hướng, tốc độ thay đổi khoảng cách của xe mô tô đối với vị trí xuất phát \(A\) là 80 m/phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.