[MĐ4] Công tử Bạc Liêu có một mảnh đất hình vuông ở một khu đô thị sầm uất, hình vuông có cạnh \(40{\rm{ m}}\), công tử dự định xây một hồ bơi được giới hạn bởi cạnh \(AB\) của hình vuông và một parabol đi qua hai đầu mút cạnh đó, đỉnh của parabol cách cạnh \(AB\) một đoạn \(10{\rm{ m}}\). Từ vị trí \(O\) là trung điểm \[AB,\] kẻ tia \(Ot\) bất kì cắt parabol và một cạnh khác của hình vuông theo thứ tự tại các điểm \(M,N\). Gọi \(P\) là trung điểm \[MN,\]khi tia \(Ot\) quay quanh gốc \(O\) thì tập hợp các điểm \(P\) tạo thành đường cong \((L)\). Công tử dự định sử dụng một loại gạch men đặc biệt để lát nền cho toàn bộ khu vực được giới hạn bởi đường cong \((L)\) và parabol. Phần còn lại trên mảnh đất hình vuông đó thì công tử sẽ trồng cỏ.
Biết rằng chi phí xây hồ bơi là \(5\) triệu đồng/\({m^2}\), chi phí lát gạch men là \(2\) triệu đồng/\({m^2}\), chi phí trồng cỏ tự nhiên là \(100\)nghìn đồng/\({m^2}\). Tính tổng số tiền mà công tử Bạc Liêu phải chi trả cho toàn bộ dự án trên theo đơn vị tỷ đồng (làm tròn đến hàng phần chục).
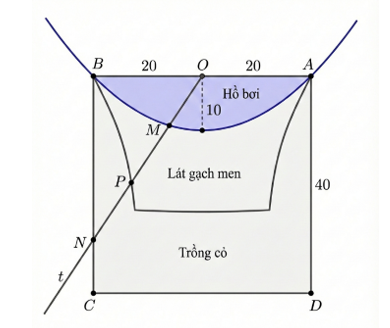
[MĐ4] Công tử Bạc Liêu có một mảnh đất hình vuông ở một khu đô thị sầm uất, hình vuông có cạnh \(40{\rm{ m}}\), công tử dự định xây một hồ bơi được giới hạn bởi cạnh \(AB\) của hình vuông và một parabol đi qua hai đầu mút cạnh đó, đỉnh của parabol cách cạnh \(AB\) một đoạn \(10{\rm{ m}}\). Từ vị trí \(O\) là trung điểm \[AB,\] kẻ tia \(Ot\) bất kì cắt parabol và một cạnh khác của hình vuông theo thứ tự tại các điểm \(M,N\). Gọi \(P\) là trung điểm \[MN,\]khi tia \(Ot\) quay quanh gốc \(O\) thì tập hợp các điểm \(P\) tạo thành đường cong \((L)\). Công tử dự định sử dụng một loại gạch men đặc biệt để lát nền cho toàn bộ khu vực được giới hạn bởi đường cong \((L)\) và parabol. Phần còn lại trên mảnh đất hình vuông đó thì công tử sẽ trồng cỏ.
Biết rằng chi phí xây hồ bơi là \(5\) triệu đồng/\({m^2}\), chi phí lát gạch men là \(2\) triệu đồng/\({m^2}\), chi phí trồng cỏ tự nhiên là \(100\)nghìn đồng/\({m^2}\). Tính tổng số tiền mà công tử Bạc Liêu phải chi trả cho toàn bộ dự án trên theo đơn vị tỷ đồng (làm tròn đến hàng phần chục).

Quảng cáo
Trả lời:
Đáp án:
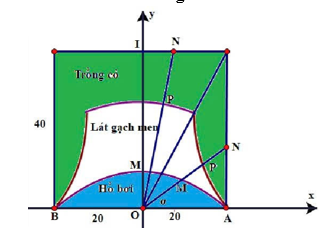
Gán hệ trục tọa độ như hình vẽ. Ta dễ dàng tìm được \((P):y = - \frac{1}{{40}}{x^2} + 10\).
Diện tích hồ bơi là: \({S_b} = 2\int\limits_0^{20} {\left( { - \frac{1}{{40}}{x^2} + 10} \right)} = \frac{{800}}{3}\).
Gọi \(\alpha \) là góc tạo bởi tia \(Ot\) và trục \(Ox\).
Lúc đó: \[M(OM\cos \alpha ;OM{\rm{ sin}}\alpha {\rm{)}}\]. Vì \[M \in \left( P \right)\]\( \Rightarrow OM{\rm{ sin}}\alpha = \frac{{ - 1}}{{40}}{\left( {OM{\rm{ cos}}\alpha } \right)^2} + 10\).
\[ \Rightarrow O{M^2}{\rm{ }}{\left( {{\rm{cos}}\alpha } \right)^2} + 40OM{\rm{ sin}}\alpha - 400 = 0 \Leftrightarrow \left[ \begin{array}{l}OM = \frac{{ - 20\sin \alpha - 20}}{{{{\left( {{\rm{cos}}\alpha } \right)}^2}}}\\OM = \frac{{ - 20\sin \alpha + 20}}{{{{\left( {{\rm{cos}}\alpha } \right)}^2}}}\end{array} \right.\].
Ta chọn \(OM = \frac{{20 - 20\sin \alpha }}{{{{\left( {{\rm{cos}}\alpha } \right)}^2}}} = \frac{{20}}{{1 + \sin \alpha }}\).
TH1: \(\alpha \in \left[ {0,\arctan 2} \right] \Rightarrow ON = \frac{{20}}{{{\rm{cos}}\alpha }}\). Suy ra: \(OP = \frac{{OM + ON}}{2} = \frac{{10}}{{1 + \sin \alpha }} + \frac{{10}}{{{\rm{cos}}\alpha }}\).
TH2: \(\alpha \in \left[ {\arctan 2,\frac{\pi }{2}} \right] \Rightarrow ON = \frac{{40}}{{{\rm{sin}}\alpha }}\). Suy ra: \(OP = \frac{{OM + ON}}{2} = \frac{{10}}{{1 + \sin \alpha }} + \frac{{20}}{{{\rm{sin}}\alpha }}\).
\[{S_{(L)}} = 2\left[ {\frac{1}{2}\int\limits_0^{\arctan 2} {{{\left( {\frac{{10}}{{1 + \sin \alpha }} + \frac{{10}}{{{\rm{cos}}\alpha }}} \right)}^2}} {\rm{d}}\alpha + \frac{1}{2}\int\limits_{\arctan 2}^{\frac{\pi }{2}} {{{\left( {\frac{{10}}{{1 + \sin \alpha }} + \frac{{20}}{{{\rm{sin}}\alpha }}} \right)}^2}} {\rm{d}}\alpha } \right] = 756,3({m^2})\].
Tổng chi phí:
\(5.{S_b} + 2.\left( {{S_L} - {S_b}} \right) + 0,1\left( {{S_V} - {S_L}} \right) = 5.\frac{{800}}{3} + 2.\left( {756,3 - \frac{{800}}{3}} \right) + 0,1\left( {1600 - 756,3} \right) = 2396,97 \approx 2,4\)tỉ.
Lưu ý: Ở trên ta sử dụng công thức của bổ đề sau:
Cho một đương cong ( \(L\) ) có phương trình trong hệ tọa độ cực là \(r = r\left( \theta \right)\), với \(\alpha \le \theta \le \beta \). Tính diện tích \(S\) của hình phẳng giới hạn bởi đường cong \(\left( L \right)\) và hai tia \(\theta = \alpha ,\theta = \beta \).
\(S = \int_\alpha ^\beta {\frac{1}{2}} {[r(\theta )]^2}d\theta \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
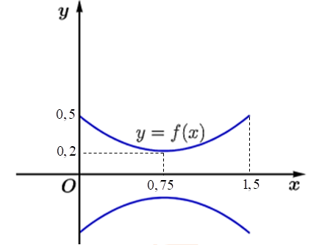
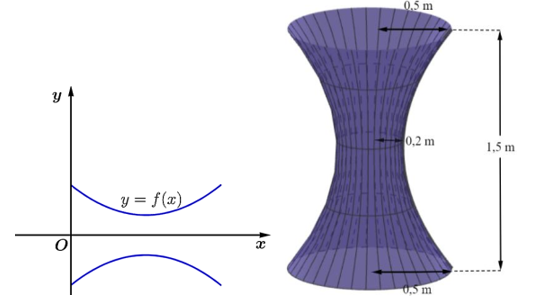
a) Gọi \(y = f\left( x \right)\)\( = a{x^2} + bx + c\).
Parabol cắt trục tung tại điểm \(\left( {0;0,5} \right)\) và đỉnh \(I\left( {0,75;0,2} \right)\)
Ta có hệ: \(\left\{ \begin{array}{l}c = 0,5\\a{\left( {0,75} \right)^2} + b.0,75 + c = 0,2\\ - \frac{b}{{2a}} = 0,75\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}c = \frac{1}{2}\\\frac{{9a}}{{16}} + \frac{{3b}}{4} + c = \frac{1}{5}\\3a + 2b = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{8}{{15}}\\b = - \frac{4}{5}\\c = \frac{1}{2}\end{array} \right.\).
Suy ra: \(f\left( x \right) = \frac{8}{{15}}{x^2} - \frac{4}{5}x + \frac{1}{2}\). Mệnh đề a) đúng.
b) Thể tích của chậu nước bằng
\(V = \pi \int\limits_0^{1,5} {{{\left[ {f\left( x \right)} \right]}^2}{\rm{d}}x} \)\( = \pi \int\limits_0^{1,5} {{{\left[ {\frac{8}{{15}}{x^2} - \frac{4}{5}x + \frac{1}{2}} \right]}^2}{\rm{d}}x} \)\( \approx 0,4618141201 \approx 0,5\). Mệnh đề b) đúng.
c) Tốc độ bơm nước vào bể \(5\) lít/phút \( = 5\,d{m^3}\)/phút \( = {5.10^{ - 3}}\,{m^3}\)/phút
Thể tích nước bơm sau \(1,5\) giờ \( = 1,5 \times 60 = 90\) phút là \({5.10^{ - 3}} \times 90 = 0,45 \approx 0,5\,\,{m^3}\). Mệnh đề c) đúng.
d) Gọi \(h\) là độ cao của nước trong chậu sau khi bơm được \(t\) phút.
Ta có: \({V_h} = \pi \int\limits_0^h {{{\left( {\frac{8}{{15}}{x^2} - \frac{4}{5}x + \frac{1}{2}} \right)}^2}{\rm{d}}x} \)\( = \pi \left( {\frac{{64}}{{1125}}{h^5} - \frac{{16}}{{75}}{h^4} + \frac{{88}}{{225}}{h^3} - \frac{2}{5}{h^2} + \frac{1}{4}h} \right)\) \({m^3}\).
Thể tích nước bơm sau \(t\) phút là \(V = 0,005t\,{m^3}\)
Khi đó: \(\pi \left( {\frac{{64}}{{1125}}{h^5} - \frac{{16}}{{75}}{h^4} + \frac{{88}}{{225}}{h^3} - \frac{2}{5}{h^2} + \frac{1}{4}h} \right) = 0,005t\) \(\left( * \right)\).
Tại thời điểm \(t = 20\) ta có: \(\pi \left( {\frac{{64}}{{1125}}{h^5} - \frac{{16}}{{75}}{h^4} + \frac{{88}}{{225}}{h^3} - \frac{2}{5}{h^2} + \frac{1}{4}h} \right) = 0,1\)\( \Rightarrow {h_0} \approx 0,1640803548\).
Đạo hàm theo biến \(t\) hai vế của \(\left( * \right)\) ta được:\(\left( {\frac{{64}}{{225}}{h^4} - \frac{{64}}{{75}}{h^3} + \frac{{264}}{{225}}{h^2} - \frac{4}{5}h + \frac{1}{4}} \right)h'\left( t \right) = \frac{{0,005}}{\pi }\)
Tốc độ dâng lên của nước
\(v\left( t \right) = h'\left( t \right) = \frac{{0,005}}{{\pi \left( {\frac{{64}}{{225}}{h^4} - \frac{{64}}{{75}}{h^3} + \frac{{264}}{{225}}{h^2} - \frac{4}{5}h + \frac{1}{4}} \right)}}\)
Tại thời điểm \(t = 20\),\({h_0} \approx 0,1640803548\) tốc độ dâng của nước là:
\(v\left( {20} \right) = h'\left( {20} \right) = \frac{{0,005}}{{\pi \left( {\frac{{64}}{{225}}h_0^4 - \frac{{64}}{{75}}h_0^3 + \frac{{264}}{{225}}h_0^2 - \frac{4}{5}{h_0} + \frac{1}{4}} \right)}}\)
\( \approx 0,01084447993\)m/phút.\( \approx 0,01\). Mệnh đề d) đúng.Lời giải
Đáp án: 80.
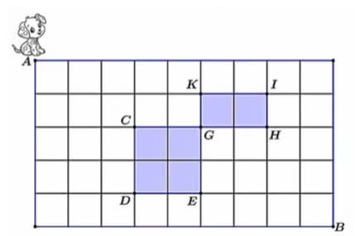
Ta có: \(A = (0;0;0)\) và \(B = (0;600;0)\).
Độ dài quãng đường \(AB\) là \(AB = \sqrt {{{(0 - 0)}^2} + {{(600 - 0)}^2} + {{(0 - 0)}^2}} = \sqrt {{0^2} + {{600}^2} + {0^2}} = 600\) (m).
Thời gian đi từ \(A\) đến \(B\) là 6 phút.
Tốc độ của xe mô tô khi đi từ \(A\) đến \(B\) là: \(v = \frac{{AB}}{6} = \frac{{600}}{6} = 100\) (m/phút).
Sau khi đổi hướng tại \(B\), xe đi từ \(B(0;600;0)\) đến \(C(1500;600;0)\) với tốc độ không đổi \(v = 100\) m/phút.
Giả sử tại thời điểm \(t\) (phút) kể từ khi đổi hướng tại \(B\), xe đang ở vị trí \(M(x;y;z)\).
Vecto chỉ phương của đoạn \(BC\) là: \({\vec u_{BC}} = \frac{{\overrightarrow {BC} }}{{|\overrightarrow {BC} |}} = \frac{{(1500 - 0;600 - 600;0 - 0)}}{{\sqrt {{{1500}^2} + {0^2} + {0^2}} }} = \frac{{(1500;0;0)}}{{1500}} = (1;0;0)\).
Vị trí của xe tại thời điểm \(t\) là: \(M(t) = B + v \cdot t \cdot {\vec u_{BC}}\)
\(M(t) = (0;600;0) + 100 \cdot t \cdot (1;0;0)\)
\(M(t) = (0 + 100t;600 + 0;0 + 0)\)
\(M(t) = (100t;600;0)\).
Khoảng cách từ xe mô tô đến vị trí xuất phát \(A(0;0;0)\) tại thời điểm \(t\) là \(D(t)\):
\(D(t) = |\overrightarrow {AM(t)} | = \sqrt {{{(100t - 0)}^2} + {{(600 - 0)}^2} + {{(0 - 0)}^2}} \)\( = \sqrt {{{(100t)}^2} + {{600}^2}} \)\( = 100\sqrt {{t^2} + 36} \).
Tốc độ thay đổi khoảng cách của xe mô tô đối với vị trí xuất phát \(A\) chính là đạo hàm của \(D\left( t \right)\) theo \(t\):
\(D'\left( t \right) = {\left( {100\sqrt {{t^2} + 36} } \right)^\prime }\)\( = 100 \cdot \frac{1}{{2\sqrt {{t^2} + 36} }} \cdot (2t)\)\( = \frac{{100t}}{{\sqrt {{t^2} + 36} }}\).
Tại phút thứ 8 kể từ khi xe đổi hướng, tức là \(t = 8\) phút.
Thay \(t = 8\) vào biểu thức \(D'\left( t \right)\) ta được:
\(D'\left( 8 \right) = \frac{{100 \cdot 8}}{{\sqrt {{8^2} + 36} }}\)\( = \frac{{800}}{{\sqrt {64 + 36} }}\)\( = \frac{{800}}{{\sqrt {100} }}\)\( = \frac{{800}}{{10}}\)\( = 80\) (m/phút).
Vậy, ở phút thứ 8 kể từ khi xe đổi hướng, tốc độ thay đổi khoảng cách của xe mô tô đối với vị trí xuất phát \(A\) là 80 m/phút.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.