Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), cạnh \(AB = a\), các cạnh bên \(SA = SB = SC = \frac{{a\sqrt 6 }}{2}\). Gọi \(H\) là trung điểm của \(BC\).
Quảng cáo
Trả lời:
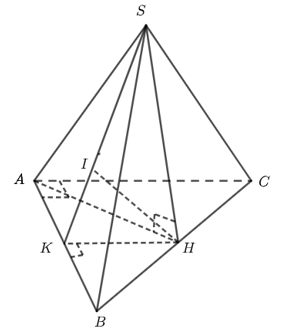
(a) [NB] Xét \(\Delta \,ABC\) vuông cân tại \(A\), nên có \(BC = \sqrt {A{B^2} + A{C^2}} = a\sqrt 2 \), và \(HA = HB = HC = \frac{{BC}}{2} = \frac{{a\sqrt 2 }}{2}\). Do đó \(H\) là tâm đường trong ngoại tiếp \(\Delta \,ABC\).
Hình chóp \(S.ABC\) có \(SA = SB = SC\), nên hình chiếu của \(S\)lên đáy là tâm của đường tròn ngoại tiếp \(\Delta \,ABC\). Suy ra \(SH \bot \left( {ABC} \right)\). Vậy (a) đúng.
(b) [TH] Xét \(\Delta \,ABC\) vuông tại \(A\), có \({S_{\Delta ABC}} = \frac{1}{2}.AB.AC = \frac{{{a^2}}}{2}\)
Xét \(\Delta \,SAH\) vuông tại \(H\) có \(SH = \sqrt {S{A^2} - A{H^2}} = \sqrt {{{\left( {\frac{{a\sqrt 6 }}{2}} \right)}^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = a\)
Vậy thể tích khối chóp \(\,S.ABC\) là: \({V_{SABC}} = \frac{1}{3}.{S_{\Delta ABC}}.SH = \frac{1}{3}.\frac{{{a^2}}}{2}.a = \frac{{{a^3}}}{6}\)\(\)(đvtt)
Vậy (b) Sai.
(c) [TH] Vì \(SH \bot \left( {ABC} \right) \Rightarrow SH \bot AH \Rightarrow \overrightarrow {SH} .\overrightarrow {AH} = 0\)
Vì \(\,\,\Delta ABC\) vuông cân tại \(A \Rightarrow AH \bot BC \Rightarrow \overrightarrow {AH} .\overrightarrow {HB} = 0\)
Tính \(\overrightarrow {AH} .\overrightarrow {SB} = \overrightarrow {AH} .\left( {\overrightarrow {SH} + \overrightarrow {HB} } \right) = \overrightarrow {AH} .\overrightarrow {SH} + \overrightarrow {AH} .\overrightarrow {HB} = 0 \Rightarrow \)\(AH \bot SB\).
Vậy (c) đúng.
(d) [TH] Khoảng cách từ điểm \(C\)đến mặt phẳng \(\left( {SAB} \right)\) bằng \(\frac{{2\sqrt 5 }}{5}a\).
Trong \(\Delta \,ABC\) kẻ \(HK \bot AB\), suy ra \(HK{\rm{//}}AC\), vậy \(HK\) là đường trung bình của \(\Delta ABC\), nên \(HK = \frac{{AC}}{2} = \frac{a}{2}\).
Khi đó có \(\left\{ \begin{array}{l}AB \bot HK\\AB \bot SH\,\,\,\left( {do\,\,\,SH \bot \left( {ABC} \right)} \right)\end{array} \right.\) \( \Rightarrow AB \bot \left( {SHK} \right)\).
Trong \(\Delta SHK\) kẻ \(HI \bot SK\, \Rightarrow \,HI \bot AB\). Vậy \(HI \bot \left( {SAB} \right)\).
Do đó \(d\left( {H,\left( {SAB} \right)} \right) = HI = \frac{{HK.HS}}{{\sqrt {H{K^2} + H{S^2}} }} = \frac{{\frac{a}{2}.a}}{{\sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {a^2}} }} = \frac{{a\sqrt 5 }}{5}\).
Vì \(H\) là trung điểm của \(BC\), nên \(d\left( {C,\left( {SAB} \right)} \right) = 2.d\left( {H,\left( {SAB} \right)} \right) = 2.HI = \frac{{2a\sqrt 5 }}{5}\)
Vậy (d) đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: \[1,5\].
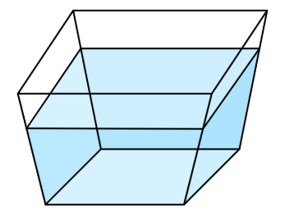
Thể tích nước sau 2 phút là \[4,75.2 = 9,5\;\left( {lit} \right) = 9,5\;\left( {d{m^3}} \right)\].
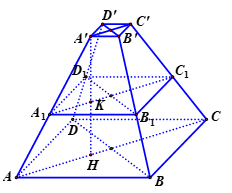
Vì lúc đầu chậu không có nước nên phần nước bơm vào chiếm chỗ bằng một khối chóp cụt tứ giác đều với cạnh đáy lần lượt là \[A'D' = 2\;\left( {dm} \right)\], \[{A_1}{D_1} = x\;\left( {dm} \right)\] và chiều cao \[A'K = h\;\left( {dm} \right)\].
Có \[AC = 4\sqrt 2 \;\left( {dm} \right),\;A'C' = 2\sqrt 2 \;\left( {dm} \right)\], suy ra \[AH = \frac{{AC - A'C'}}{2} = \frac{{4\sqrt 2 - 2\sqrt 2 }}{2} = \sqrt 2 \;\left( {dm} \right)\]
Và \[{A_1}{C_1} = x\sqrt 2 \;\left( {dm} \right)\], suy ra \[{A_1}K = \frac{{{A_1}{C_1} - A'C'}}{2} = \frac{{x\sqrt 2 - 2\sqrt 2 }}{2}\;\left( {dm} \right)\].
Mặt khác, trong tam giác \[A'AH\] theo Ta-lét có \[\frac{{{A_1}K}}{{AH}} = \frac{{A'K}}{{A'H}} \Leftrightarrow \frac{{\frac{{x\sqrt 2 - 2\sqrt 2 }}{2}}}{{\sqrt 2 }} = \frac{h}{3} \Leftrightarrow h = 3.\frac{{x - 2}}{2}\].
Có \[{V_{{A_1}{B_1}{C_1}{D_1}.A'B'C'D'}} = \frac{1}{3}h.\left( {{x^2} + {2^2} + \sqrt {{x^2}{{.2}^2}} } \right) = 9,5\]\[ \Leftrightarrow \frac{{x - 2}}{2}.\left( {{x^2} + 4 + 2x} \right) = 9,5\]\[ \Leftrightarrow x = 3\].
Vậy \[h = 3.\frac{{3 - 2}}{2} = 1,5\].
Lời giải
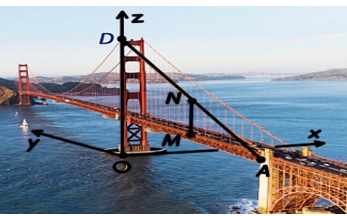
Gọi các đỉnh của đoạn dây điện như ở hình vẽ này:
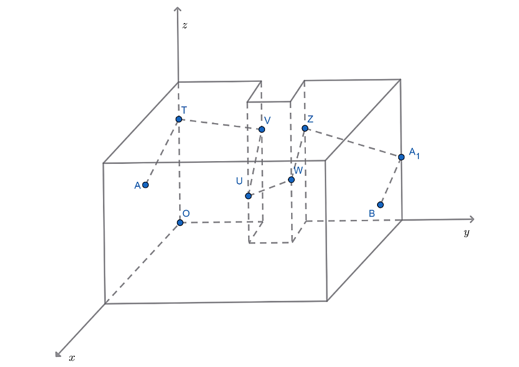
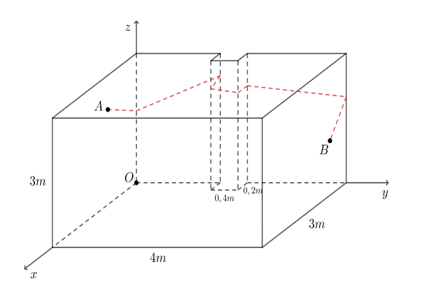
Trải tường chứa \(A\); tường chứa \(B\);các mặt của cột lên mặt phẳng \(Oyz\) ta có hình vẽ sau:
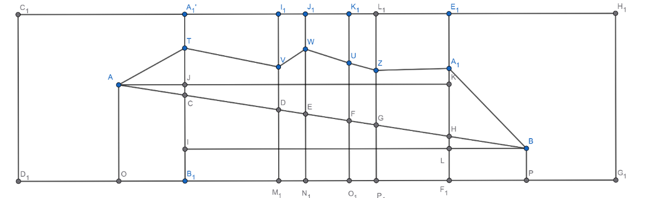
Ta nhận thấy như sau: Khi trải phẳng hình như trên; độ dài của đoạn dây điện vẫn được bảo toàn; đồng thời nhìn vào hình vẽ trên ta thấy được độ dài đoạn dây điện sẽ lớn hơn hoặc bằng độ dài đoạn \(AB\) khi trải hình như trên. Như vậy; ta đi tính độ dài đoạn \(AB\) khi trai hình như trên.
Lấy \(O'\) là hình chiếu của \(A\) lên \({B_1}{D_1}.\) \(P\) là hình chiếu của \(B\) lên \({F_1}{G_1}.\)
Khi đó \(AO'\) ở hình vẽ trên cũng chính bằng khoảng cách từ điểm \(A\) của đề lên \(Oy\) và nó cũng bằng \(2,5\). Tương tự \(BP = 1\).
\(O'{B_1}\) sẽ bằng khoảng cách từ \(A\) đến \(Oz\) và bằng \(1\). Tương tự \({F_1}P = 0,5.\)
Ta có độ dài \({B_1}{F_1} = {A_1}{I_1} + {I_1}{J_1} + {J_1}{K_1} + {K_1}{L_1} + {L_1}{E_1} = 4 + 0,2.2 = 4,4 \Rightarrow O'P = 1,5 + 4,4 = 5,9\).
Do đó nên theo định lý Pytago ta có \(AB = \sqrt {O'{P^2} + {{\left( {AO' - BP} \right)}^2}} \approx 6,09\).
Vậy nên độ dài đoạn dây điện tối thiểu xấp xỉ \(6,09\;\)m.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.