Cho tỉ lệ thức \(\frac{{3a + 2b + c}}{{a + 2b - c}} = \frac{{3a - 2b + c}}{{a - 2b - c}}\,\,(b \ne 0)\).
Chứng minh rằng \(a + c = 0\).
Cho tỉ lệ thức \(\frac{{3a + 2b + c}}{{a + 2b - c}} = \frac{{3a - 2b + c}}{{a - 2b - c}}\,\,(b \ne 0)\).
Chứng minh rằng \(a + c = 0\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 2 Toán 7 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\[\frac{{3a + 2b + c}}{{a + 2b - c}} = \frac{{3a - 2b + c}}{{a - 2b - c}}\,\, = \frac{{\left( {3a + 2b + c} \right) - \left( {3a - 2b + c} \right)}}{{\left( {a + 2b - c} \right) - \left( {a - 2b - c} \right)}}\]
\[ = \frac{{3a + 2b + c - 3a + 2b - c}}{{a + 2b - c - a + 2b + c}} = \frac{{\left( {3a - 3a} \right) + \left( {2b + 2b} \right) + \left( {c - c} \right)}}{{\left( {a - a} \right) + \left( {2b + 2b} \right) + \left( {c - c} \right)}} = \frac{{4b}}{{4b}} = 1\,\,(b \ne 0)\].
Khi đó \(\left\{ \begin{array}{l}3a + 2b + c = a + 2b - c\\3a - 2b + c = a - 2b - c\end{array} \right.\)
Suy ra \(\left( {3a + 2b + c} \right) + \left( {3a - 2b + c} \right) = \left( {a + 2b - c} \right) + \left( {a - 2b - c} \right)\)
\(3a + 2b + c + 3a - 2b + c = a + 2b - c + a - 2b - c\)
\(\left( {3a + 3a} \right) + \left( {2b - 2b} \right) + \left( {c + c} \right) = \left( {a + a} \right) + \left( {2b - 2b} \right) - \left( {c + c} \right)\)
\(6a + 2c = 2a - 2c\)
\(6a - 2a + 2c + 2c = 0\)
\(4a + 4c = 0\)
Do đó \(a + c = 0\) (đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Khối lượng của 10 cái bánh chưng là:
\(10\,\,.\,\,0,75 = 7,5\) (kg).
Gọi \(x,\,\,y\) (kg) lần lượt là khối lượng gạo nếp và đậu xanh cần để gói 10 cái bánh chưng \(\left( {0 < x,\,\,y < 7,5} \right)\).
Tỉ số giữa khối lượng gạo nếp và đậu xanh của bánh chưng là:
\(\frac{x}{y} = \frac{{0,6}}{{0,15}} = \frac{4}{1}\) hay \(\frac{x}{4} = \frac{y}{1}\).
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{4} = \frac{y}{1} = \frac{{x + y}}{{4 + 1}} = \frac{{7,5}}{5} = 1,5\).
Suy ra \(x = 1,5\,\,.\,\,4 = 6;\,\,y = 1,5\,\,.\,\,1 = 1,5\) (thỏa mãn).
Cứ 1 kg gạo nếp sau khi ngâm nặng khoảng 1,5 kg; 1 kg đậu xanh sau khi ngâm và nấu chín được khoảng 1,5 kg. Khi đó:
• Khối lượng gạo nếp cần là: \(6:1,5 = 4\) (kg);
• Khối lượng gạo nếp cần là: \(1,5:1,5 = 1\) (kg)
Vậy để làm 10 cái bánh chưng thì bạn Dương cần 4 kg gạo và 1 kg đậu xanh.
Lời giải
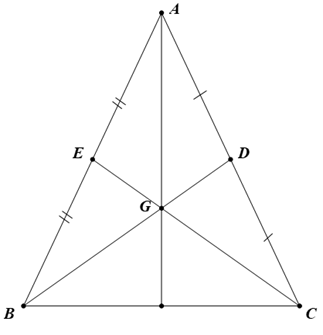
a) Vì \(G\) là giao điểm của hai đường trung tuyến\(BD\) và \(CE\) nên \(G\) là trọng tâm của tam giác \(ABC\).
Khi đó ta có: \({\rm{BG\; = \;}}\frac{2}{3}BD;\)\(\;CG = \;\frac{2}{3}CE\).
Mà \[BD = CE\] (giả thiết) nên \[BG = CG\].
Ta có \(BD = BG + DG;\,\,CE = CG + EG\) nên \[GD = GE\].
Vậy \(BG = CG;\,\,DG = GE\).
b) Xét \(\Delta BGE\) và \(\Delta CGD\) có:
\(BG = CG\) (chứng minh trên)
\[\widehat {BGE} = \widehat {CGD}\] (hai góc đối đỉnh)
\(DG = GE\) (chứng minh trên)
Do đó \(\Delta BGE = \Delta CGD\;\)(c.g.c)
Suy ra \(BE = CD\) (hai cạnh tương ứng).
Mà \(BE = \frac{1}{2}AB,\)\(CD = \frac{1}{2}AC\;\)(vì \(BD\) và \(CE\) là đường trung tuyến).
Do đó \(AB = AC\).
Vậy \(\Delta ABC\)là tam giác cân.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.