Lần lượt tác dụng các lực F1 = Focos(12πt) (N); F2 =Focos(14πt) (N); F3 = Focos(16πt) (N); F4= Focos(18πt) (N) vào con lắc lò xo có độ cứng k = 100N/m; khối lượng m = 100g. Lực làm cho con lắc dao độn...

Chọn C + Từ biểu thức của các lực => f1 = 6Hz; f2 = 7Hz; f3 = 8Hz; f4 = 9Hz. + Tần số dao động riêng của con lắc lò xo: + Với mỗi lực tác dụng trên ta có biên độ tương ứng là A1, A2, A3, A4. Trong đó Ao = Amax. + Từ đồ thị suy ra f4 làm cho con lắc dao động với Amin. Chú ý: f càng gần fo thì A càng có giá trị gần bằng Amax.

Câu hỏi:

29/09/2022 6,648

Lần lượt tác dụng các lực F₁ = F_ocos(12πt) (N); F₂ =F_ocos(14πt) (N); F₃ = F_ocos(16πt) (N); $F_{4}$ = F_ocos(18πt) (N) vào con lắc lò xo có độ cứng k = 100N/m; khối lượng m = 100g. Lực làm cho con lắc dao động với biên độ nhỏ nhất là:

A. F₁ = F_ocos(12πt) (N).

B. F₂ =F_ocos(14πt) (N).

C. F₃ = F_ocos(16πt) (N).

D. F₁ = F_ocos(18πt) (N).

Xem lời giải

Câu hỏi trong đề: 150 câu trắc nghiệm Dao động cơ nâng cao !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn C

Lần lượt tác dụng các lực F1 = Fo cos (12 pi t) (N) (ảnh 1)

+ Từ biểu thức của các lực => f₁ = 6Hz; f₂ = 7Hz; f₃ = 8Hz; f₄ = 9Hz.

+ Tần số dao động riêng của con lắc lò xo: Lần lượt tác dụng các lực F1 = Fo cos (12 pi t) (N) (ảnh 2)

+ Với mỗi lực tác dụng trên ta có biên độ tương ứng là A₁, A₂, A₃, A₄. Trong đó A_o = A_max.

+ Từ đồ thị suy ra f₄ làm cho con lắc dao động với A_min.

Chú ý: f càng gần f_o thì A càng có giá trị gần bằng A_max.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một con lắc lò xo gồm vật nhỏ khối lượng 0,2kg và lò xo có độ cứng 20N/m. Vật nhỏ được đặt trên giá cố định nằm ngang dọc theo trục nằm ngang. Hệ số ma sát trượt giữa giá đỡ và vật nhỏ là 0,01. Từ vị trí lò xo không biến dạng truyền cho vật vận tốc đầu 1m/s thì thấy con lắc dao động tắt dần trong giới hạn đàn hồi của lò xo. Độ lớn của lực đàn hồi cực đại của lò xo trong quá trình dao động là:

A. 19,8N

B. 1,5N

C. 2,2N

D. 1,98N

Lời giải

Chọn D

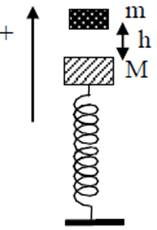
+ Gọi A là biên độ cực đại của dao động. Khi đó lực đàn hồi cực đại của lò xo trong quá trình dao động F_max = kA.

+ Để tìm A ta dựa vào định luật bảo toàn năng lượng:

+ Thay số, lấy g = 10m/s² ta được phương trình: 0,1 = 10A² + 0,02A => A = 0,099m (loại nghiệm âm).

+ Do đó F_max = kA = 1,98N.

Câu 2

Một chất điểm dao động điều hòa không ma sát. Khi vừa qua khỏi vị trí cân bằng một đoạn S, động năng của chất điểm là 1,8J. Đi tiếp một đoạn S nữa thì động năng chỉ còn 1,5J và nếu đi thêm một đoạn S nữa thì động năng bây giờ là:

A. 0,9J.

B. 1,0J.

C. 0,8J.

D. 1,2J.

Lời giải

Chọn B

+ Ta luôn có W_đ1 + W_t1 =W_đ2 + W_t2 = W_đ3 + W_t3 = E = hằng số (1).

+ Xét Một chất điểm dao động điều hòa không ma sát. Khi vừa qua khỏi vị trí (ảnh 1)

=> W_t2 = 4W_t1 (2).

+ Từ (1) ta có 1,8 + W_t1 = 1,5 + W_t2 (3).

Giải hệ (2) và (3) ta được W_t1 = 0,1J và W_t2 = 0,4J => E = 1,9J.

+ Xét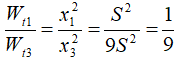

=> W_t2 = 9W_t1 = 0,9J. => W_đ3 = – W_t3 = 1,9 – 0,9 = 1,0J.

Câu 3

Một con lắc lò xo đặt nằm ngang gồm vật M có khối lượng 400g và lò xo có hệ số cứng 40N/m đang dao động điều hòa xung quanh vị trí cân bằng với biên độ 5cm. Khi M qua vị trí cân bằng người ta thả nhẹ vật m có khối lượng 100g lên M (m đính chặt ngay vào M), sau đó hệ m và M dao động với biên độ:

A. 2√5cm.

B. 4,25cm.

C. 3√2cm.

D. 2√2cm.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Con lắc lò xo gồm vật nặng M = 300g, lò xo có độ cứng k = 200N/m, lồng vào một trục thẳng đứng như hình vẽ. Khi M đang ở vị trí cân bằng thì vật m = 200g từ độ cao h = 3,75m so với M rơi tự do, va chạm mềm với M, coi ma sát là không đáng kể, lấy g = 10m/s². Sau va chạm hai vật cùng dao động điều hòa, chọn gốc tọa độ tại vị trí cân bằng của hệ, chiều dương như hình vẽ, gốc thời gian t = 0 là lúc va chạm. Phương trình dao động của hệ hai vật là:

A. x = 1,08cos(20t + 0,378) cm.

B. x = 2,13cos(20t + 1,093) cm.

C. x = 1,57cos(20t + 0,155) cm.

D. Đáp án khác

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một con lắc lò xo thẳng đứng gồm lò xo nhẹ có độ cứng k = 100N/m, một đầu cố định, một đầu gắn vật nặng khối lượng m = 0,5kg. Ban đầu kéo vật theo phương thẳng đứng khỏi vị trí cân bằng 5cm rồi buông nhẹ cho dao động. Trong quá trình dao động vật luôn chịu tác dụng của lực cản có độ lớn bằng 1/100 trọng lực tác dụng lên vật. Coi biên độ của vật giảm đều trong từng chu kì, lấy g = 10m/s². Số lần vật qua vị trí cân bằng kể từ khi thả vật tới khi dừng hẳn là:

A. 25

B. 50

C. 75

D. 100

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Con lắc lò xo gồm vật nhỏ có khối lượng m = 1kg và lò xo nhẹ có độ cứng k = 100N/m được treo thẳng đứng vào một điểm cố định. Vật được đặt trên một giá đỡ D. Ban đầu giá đỡ D đứng yên và lò xo giãn 1cm. Cho D chuyển động nhanh dần đều thẳng đứng xuống dưới với gia tốc a = 1m/s². Bỏ qua mọi ma sát và lực cản, lấy g = 10m/s². Sau khi rời khỏi giá đỡ, vật m dao động điều hòa với biên độ xấp xỉ bằng:

A. 6,08cm.

B. 9,80cm.

C. 5,74cm.

D. Đáp án khác

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Một con lắc lò xo gồm lò xo có độ cứng k = 100N/m và vật nặng có khối lượng m = 5/9 kg đang dao động điều hòa theo phương ngang với biên độ 2cm trên mặt phẳng nhẵn nằm ngang. Tại thời điểm m qua vị trí động năng bằng thế năng, một vật nhỏ có khối lượng m_o = 0,5m rơi thẳng đứng và dính chặt vào m. Khi qua vị trí cân bằng hệ (m + m_o) có tốc độ bằng:

A. 20cm/s.

B. 30√3cm/s.

C. 25cm/s.

D. 5√12cm/s.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Lần lượt tác dụng các lực F1 = Focos(12πt) (N); F2 =Focos(14πt) (N); F3 = Focos(16πt) (N); F4= Focos(18πt) (N) vào con lắc lò xo có độ cứng k = 100N/m; khối lượng m = 100g. Lực làm cho con lắc dao động với biên độ nhỏ nhất là:

Bình luận

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Lần lượt tác dụng các lực F₁ = F_ocos(12πt) (N); F₂ =F_ocos(14πt) (N); F₃ = F_ocos(16πt) (N); $F_{4}$ = F_ocos(18πt) (N) vào con lắc lò xo có độ cứng k = 100N/m; khối lượng m = 100g. Lực làm cho con lắc dao động với biên độ nhỏ nhất là: