Câu hỏi:
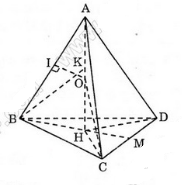
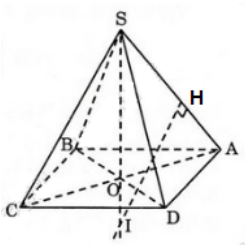
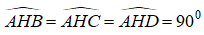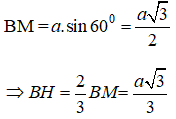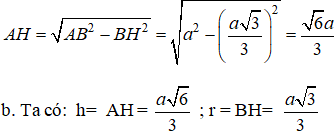13/07/2024 17,039Cho tứ diện đều ABCD cạnh a. Gọi H là hình chiếu vuông góc của đỉnh A xuống mặt phẳng (BCD).
Chứng minh H là tâm đường tròn ngoại tiếp tam giác BCD. Tính độ dài đoạn AH.
Câu hỏi trong đề: Giải bài tập Hình học 12 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Từ A vẽ AH ⊥ (BCD)
Xét ba tam giác ABH, ACH và ADH có:
AB= AC = AD ( vì ABCD là tứ diện đều).
AH chung
=> ∆ ABH = ∆ ACH =∆ ADH ( ch- cgv)
Suy ra,HB = HC = HD . Do đó, H là tâm đường tròn ngoại tiếp tam giác BCD
Do tam giác BCD là tam giác đều nên H đồng thời là trọng tâm tam giác BCD
Gọi M là trung điểm CD. Ta có;
+ xét tam giác AHB vuông tại H có:
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình vuông ABCD cạnh a. Từ tâm O của hình vuông dựng đường thẳng Δ vuông góc với mặt phẳng (ABCD). Trên Δ lấy điểm S sao cho OS = a/2 . Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. Tính diện tích mặt cầu và thể tích khối cầu được tạo nên bởi mặt cầu đó.
Xem đáp án »
13/07/2024
4,724
Câu 2:
Một hình chóp có tất cả các cạnh bên bằng nhau. Chứng minh rằng hình chóp đó nội tiếp được trong một mặt cầu (các đỉnh của hình chóp nằm trên mặt cầu).
Xem đáp án »
13/07/2024
4,357
Câu 3:
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC) và cạnh BD vuông góc với cạnh BC. Biết AB = AD = a. Tính diện tích xung quanh của hình nón và thể tích của khối nón được tạo thành khi quay đường gấp khúc BDA quanh cạnh AB.
Xem đáp án »
13/07/2024
4,125
Câu 4:
Hình chóp S.ABC có một mặt cầu tiếp xúc với các cạnh bên SA, SB, SC. Mặt cầu này còn tiếp xúc với ba cạnh AB, BC, CA tại trung điểm của mỗi cạnh. Chứng minh rằng hình chóp đó là hình chóp tam giác đều.
Xem đáp án »
13/07/2024
2,457
Câu 5:
Cho hình trụ có bán kính r, trục OO' = 2r và mặt cầu đường kính OO'.
Hãy so sánh diện tích mặt cầu và diện tích xung quanh của hình trụ.
Xem đáp án »
13/07/2024
1,276
Câu 6:
Cho hình trụ có bán kính r, trục OO' = 2r và mặt cầu đường kính OO'.
Hãy so sánh thể tích khối trụ và thể tích khối cầu được tạo nên bởi hình trụ và mặt cầu đã cho.
Xem đáp án »
13/07/2024
1,249
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận