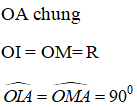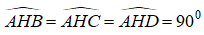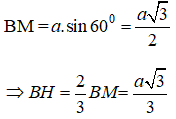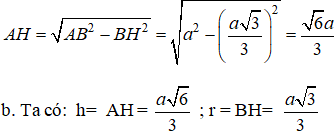Ôn tập chương 2 Hình học 12
37 người thi tuần này 4.6 19 K lượt thi 9 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Lê Trọng Tấn (TP.HCM) có đáp án
Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Thủ Đức (TP.HCM) có đáp án
Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Ngô Quyền (TP.HCM) có đáp án
Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Mạc Đĩnh Chi (TP.HCM) có đáp án
Đề thi cuối kì 1 Toán 12 năm 2025-2026 THCS - THPT Trần Cao Vân (TP.HCM) có đáp án
Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Bùi Thị Xuân (TP.HCM) có đáp án
Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Marie Curie (TP.HCM) có đáp án
Đề thi cuối kì 1 Toán 12 năm 2025-2026 THPT Nguyễn Thị Minh Khai (TP.HCM) có đáp án
Danh sách câu hỏi:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Đúng
b) Sai
c) Sai
d) Đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Cho hình chóp
có các cạnh bên bằng nhau.
Gỉa sử I là hình chiếu vuông góc của S trên mặt đáy.
được trong một đường tròn tâm I bán kính IA, trục SI.
Trong mp(SAI), đường trung trực
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
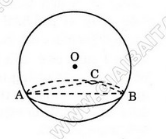
Gọi mặt cầu đã cho có tâm O và bán kính R.
Gọi M, N, P lần lượt là trung điểm của AB, BC và CA.
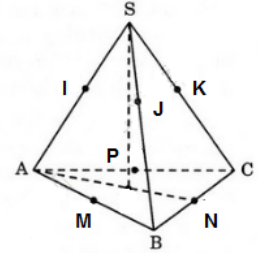
Gọi I,J và K lần lượt là tiếp điểm của các cạnh bên SA, SB, SC với mặt cầu:
+ Từ giả thiết ta suy ra: OI ⊥ SA; OM ⊥ AB
Xét tam giác OIA và tam giác OMA có:
⇒ ∆ OIA = ∆OMA ( ch- cgv)
⇒ AM = AI.
Chứng minh tương tự có: BM= BJ và SI = SJ (1)
Mà AM = BM nên AI= BJ ; (2)
Từ (1) và (2) suy ra: SI+IA = SJ + BJ hay SA = SB (3)
* Chứng minh tương tự, ta có SB= SC (4).
Từ (3) và (4) suy ra: SA = SB = SC (*)
Mặt khác ; BM = BN (= BJ) và CN = CP (= CK)
Suy ra; AB = 2BM = BC = 2 CN = 2CP = CA
Do đó, tam giác ABC là tam giác đều (**)
Từ (*) và (**) suy ra, S. ABC là hình chóp tam giác đều.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
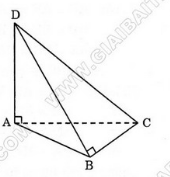
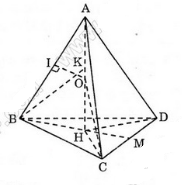
Từ A vẽ AH ⊥ (BCD)
Xét ba tam giác ABH, ACH và ADH có:
AB= AC = AD ( vì ABCD là tứ diện đều).
AH chung
=> ∆ ABH = ∆ ACH =∆ ADH ( ch- cgv)
Suy ra,HB = HC = HD . Do đó, H là tâm đường tròn ngoại tiếp tam giác BCD
Do tam giác BCD là tam giác đều nên H đồng thời là trọng tâm tam giác BCD
Gọi M là trung điểm CD. Ta có;
+ xét tam giác AHB vuông tại H có:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Diện tích xung quanh của hình trụ là:
Thể tích của khối trụ là;
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 3/9 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập