Câu hỏi:
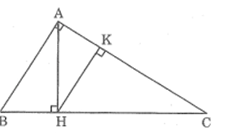
27/04/2020 872Tam giác vuông ABC có và đường cao AH. Từ H hạ HK vuông góc vói AC. Trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau?
Câu hỏi trong đề: Giải Sách Bài Tập Toán 8 Tập 2 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Trong hình trên có 5 tam giác đồng dạng với nhau theo từng đôi một đó là: ABC; HBA; HAC; KAH; KHC.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
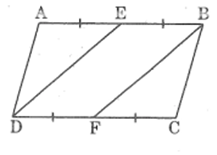
Vì ABCD là hình bình hành nên:
AB = CD (1)
Theo giả thiết:
AE = EB = 1/2 AB (2)
DF = FC = 1/2 CD (3)
Từ (1), (2) và (3) suy ra:
EB = DF và BE // DF.
Suy ra tứ giác BEDF là hình bình hành (vì có cặp cạnh đối song song và bằng nhau)
Suy ra: DE // BF
Ta có: (AED) =(ABF ) (đồng vị)
(ABF) = (BFC) (so le trong)
Suy ra: (AED) = ( BFC)
Xét AED'và CFB ta có:
(AED) =( BFC) (chứng minh trên)
A = C (tính chất hình bình hành)
Vậy: AED đồng dạng CFB (g.g)
Lời giải
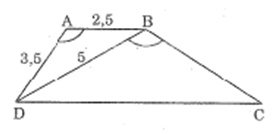
Xét ABD và BDC, ta có:
(DAB) = (DBC) (gt)
(ABD) = (BDC) (so le trong)
Suy ra: ABD ∼ BDC (g.g)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 4
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
-
Dạng 8: Bài luyện tập 3 dạng 4. Tổng hợp có đáp án