Câu hỏi:

13/07/2024 3,019

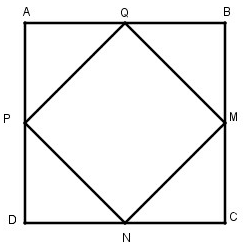
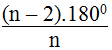Cho hình vuông ABCD. Gọi M, N, P, Q tương ứng là trung điểm của các cạnh BC, CD, DA, AB. Chứng minh MNPQ là hình vuông (tứ giác đều)

Xem lời giải

Câu hỏi trong đề: Giải Sách Bài Tập Toán 8 Tập 1 !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Do ABCD là hình vuông có M, N, P, Q lần lượt là trung điểm của BC, CD, DA, AB nên: AQ = QB = BM = MC= CN = ND = DP = PA

Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Xét Δ APQ và Δ BQM:

AQ = BM (gt)

$∠$ A = $∠$ B = $90^{0}$

AP = BQ (gt)

Do đó: $△$ APQ = $△$ BQM (c.g.c) ⇒ PQ = QM (1)

Xét $△$ BQM và $△$ CMN:

BM = CN (gt)

$∠$ B = $∠$ C = $90^{0}$

BQ = CM (gt)

Do đó: $△$ BQM = $△$ CMN (c.g.c) ⇒ QM = MN (2)

Xét $△$ CMN và $△$ DNP:

CN = DP (gt)

$∠$ C = $∠$ D = $90^{0}$

CM = DN (gt)

Do đó: $△$ CMN = $△$ DNP (c.g.c) ⇒ MN = NP (3)

Từ (1), (2) và (3) suy ra: MN = NP = PQ = QM

nên tứ giác MNPQ là hình thoi

Vì AP = AQ nên $△$ APQ vuông cân tại A

BQ = BM nên $△$ BMQ vuông cân tại B

⇒ $∠$ (AQP) = $∠$ (BQM) = $45^{0}$

$∠$ (AQP) + $∠$ (PQM) + $∠$ (BQM) = $180^{0}$ (kề bù)

⇒ $∠$ (PQM) = $180^{0}$ - ( $∠$ (AQP) + $∠$ (BQM) )

= $180^{0}$ - ( $45^{0}$ + $45^{0}$ ) = $90^{0}$

Vậy tứ giác MNPQ là hình vuông.

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Vẽ hình và tính số đường chéo của ngũ giác, lục giác

Xem đáp án

Lời giải

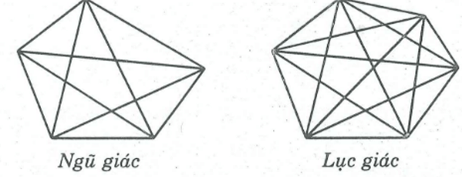
Từ mỗi đỉnh của ngũ giác vẽ được 2 đường chéo. Ngũ giác có 5 đỉnh ta kẻ được 5.2=10 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy ngũ giác có tất cả 5 đường chéo.

Từ mỗi đỉnh của lục giác vẽ được 3 đường chéo. Lục giác có 6 đỉnh ta kẻ được 6.3 = 18 đường chéo, trong đó mỗi đường chéo được tính hai lần. Vậy lục giác có tất cả 9 đường chéo.

Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

Câu 2

Tính số đo của hình 8 cạnh đều, 10 cạnh đều, 12 cạnh đều.

Xem đáp án

Lời giải

Công thức tính số đo mỗi góc của đa giác đều có n cạnh: Giải sách bài tập Toán 8 | Giải bài tập Sách bài tập Toán 8

- Đa giác đều 8 cạnh ⇒ n = 8, số đo mỗi góc là: ((8 – 2). $180^{0}$ ) / 8 = $135^{0}$

- Đa giác đều 10 cạnh ⇒ n = 10, số đo mỗi góc là: ((10 – 2). $180^{0}$ ) / 10 = $144^{0}$

- Đa giác đều 12 cạnh ⇒ n = 12, số đo mỗi góc là: ((12 – 2). $180^{0}$ ) / 12 = $150^{0}$

Câu 3