Câu hỏi:

10/05/2020 4,022

Lớp 11B có 25 đoàn viên trong đó 10 nam và 15 nữ. Chọn ngẫu nhiên 3 đoàn viên trong lớp để tham dự hội trại ngày 26 tháng 3. Tính xác suất để 3 đoàn viên được chọn có 2 nam và 1 nữ

A. $\frac{7}{920}$

B. $\frac{27}{92}$

C. $\frac{3}{115}$

D. $\frac{9}{92}$

Xem lời giải

Câu hỏi trong đề: Tổng hợp đề thi thử thpt quốc gia môn Toán hay nhất có lời giải chi tiết !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án B

Phương pháp: Công thức tính xác suất của biến cố A là: $P (A) = \frac{n_{A}}{n_{Ω}}$

Cách giải:

Chọn 3 đoàn viên trong 25 đoàn viên nên $n_{Ω} = C_{25}^{3} = 2300.$

Gọi biến cố A: “Chọn 3 đoàn viên trong đó có 2 nam và 1 nữ”.

Khi đó ta có: $n_{A} = C_{25}^{1} . C_{10}^{2} = 675.$ Vậy xác suất cần tìm là: $P (A) = \frac{n_{A}}{n_{Ω}} = \frac{675}{2300} = \frac{27}{92} .$

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

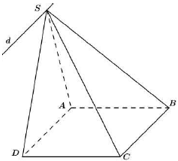
Cho hình chóp SABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC). Khẳng định nào sau đây là khẳng định đúng?

A. d qua S và song song với BD

B. d qua S và song song với BC

C. d qua S và song song với AB

D. d qua S và song song với DC

Lời giải

Đáp án B

Phương pháp:

+) Chứng minh hai mặt phẳng (SAD) và (SBC) là hai mặt phẳng có chứa hai đường thẳng song song.

+) Tìm giao tuyến d của hai mặt phẳng có chứa hai đường thẳng song song.

Cách giải:

Tứ giác ABCD là hình bình hành $\Rightarrow A D / / B C .$

Điểm S thuộc cả 2 mặt phẳng (SAD) và (SBC)

Giao tuyến của hai mặt phẳng (SAD) và (SBC) là đường thẳng d đi qua S và song song với AD, BC.

Câu 2

Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và $S A = a; S B = a \sqrt{2}, S C = a \sqrt{3}$ . Tính khoảng cách từ S đến mặt phẳng (ABC).

A. $\frac{11 a}{6}$

B. $\frac{a \sqrt{66}}{6}$

C. $\frac{6 a}{11}$

D. $\frac{a \sqrt{66}}{11}$

Lời giải

Đáp án D

Phương pháp:

- Gọi H là trực tâm tam giác, chứng minh $S H ⊥ (A B C)$ bằng cách sử dụng định lý: “Đường thẳng vuông góc với hai đường thẳng cắt nhau thì nó vuông góc với mặt phẳng chứa hai đường thẳng đó”.

- Tính độ dài SH bằng cách sử dụng hệ thức lượng giữa cạnh và đường cao trong tam giác vuông.

Cách giải: Gọi H là trực tâm của tam giác ABC.

Ta sẽ chứng minh SH là đường cao của hình chóp.

Gọi E, D lần lượt là hình chiếu của B,A lên AC,BC.

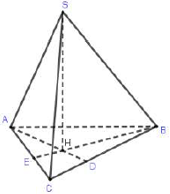
Chú ý khi giải: Từ nay về sau, các em có thể ghi nhớ hệ thức liên hệ giữa đường cao và cạnh trong hình chóp S.ABC mà có SA, SB, SC đôi một vuông góc, đó là $\frac{1}{S H^{2}} = \frac{1}{S A^{2}} \frac{1}{S B^{2}} + \frac{1}{S C^{2}}$

Câu 3

Cho hình nón có bán kính đáy là $r = \sqrt{3}$ và độ dài đường sinh l = 4 .Tính diện tích xung quanh S của hình nón đã cho

A. $S = 8 \sqrt{3} π$

B. $S = 24 π$

C. $S = 16 \sqrt{3} π$

D. $S = 4 \sqrt{3} π$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hình trụ có hai đáy là hình tròn (O) và (O’), chiều cao $R \sqrt{3},$ bán kính R và hình nón có đỉnh là O’, đáy là hình tròn $(O; R)$ . Tính tỉ số giữa diện tích xung quanh của hình trụ và diện tích xung quanh của hình nón.

C. $\sqrt{2}$

D. $\sqrt{3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hàm số $y = f (x)$ với đạo hàm $f' (x)$ có đồ thị như hình vẽ. Hàm số $g (x) = f (x) - \frac{x^{3}}{3} + x^{2} - x + 2$ đạt cực đại tại điểm nào ?

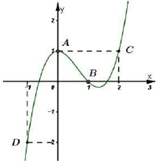
A. x = -1

B. x = 1

C. x = 0

D. x = 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Tính đạo hàm của hàm số $y = \log_{5} (x^{2} + 2) .$

A. $y' = \frac{1}{(x^{2} + 2) \ln 5}$

B. $y' = \frac{2 x}{(x^{2} + 2)}$

C. $y' = \frac{2 x \ln 5}{(x^{2} + 2)}$

D. $y' = \frac{2 x}{(x^{2} + 2) \ln 5}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Tìm giá trị lớn nhất của hàm số $y = x^{4} - 2 x^{2} - 15$ trên đoạn [-3;2]

A. $\max_{[- 3; 2]} y = 54$

B. $\max_{[- 3; 2]} y = 7$

C. $\max_{[- 3; 2]} y = 48$

D. $\max_{[- 3; 2]} y = 16$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Lớp 11B có 25 đoàn viên trong đó 10 nam và 15 nữ. Chọn ngẫu nhiên 3 đoàn viên trong lớp để tham dự hội trại ngày 26 tháng 3. Tính xác suất để 3 đoàn viên được chọn có 2 nam và 1 nữ

Bình luận

Cho hình chóp SABCD có đáy ABCD là hình bình hành. Gọi d là giao tuyến của hai mặt phẳng (SAD) và (SBC). Khẳng định nào sau đây là khẳng định đúng?

Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và SA=a;SB=a2,SC=a3. Tính khoảng cách từ S đến mặt phẳng (ABC).

Cho hình nón có bán kính đáy là r=3và độ dài đường sinh l = 4 .Tính diện tích xung quanh S của hình nón đã cho

Cho hình trụ có hai đáy là hình tròn (O) và (O’), chiều cao R3, bán kính R và hình nón có đỉnh là O’, đáy là hình tròn O;R. Tính tỉ số giữa diện tích xung quanh của hình trụ và diện tích xung quanh của hình nón.

Cho hàm số y=fxvới đạo hàm f'x có đồ thị như hình vẽ. Hàm số gx=fx−x33+x2−x+2 đạt cực đại tại điểm nào ?

Tính đạo hàm của hàm số y=log5x2+2.

Tìm giá trị lớn nhất của hàm số y=x4−2x2−15 trên đoạn [-3;2]

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc và $S A = a; S B = a \sqrt{2}, S C = a \sqrt{3}$ . Tính khoảng cách từ S đến mặt phẳng (ABC).

Cho hình nón có bán kính đáy là $r = \sqrt{3}$ và độ dài đường sinh l = 4 .Tính diện tích xung quanh S của hình nón đã cho

Cho hình trụ có hai đáy là hình tròn (O) và (O’), chiều cao $R \sqrt{3},$ bán kính R và hình nón có đỉnh là O’, đáy là hình tròn $(O; R)$ . Tính tỉ số giữa diện tích xung quanh của hình trụ và diện tích xung quanh của hình nón.

Cho hàm số $y = f (x)$ với đạo hàm $f' (x)$ có đồ thị như hình vẽ. Hàm số $g (x) = f (x) - \frac{x^{3}}{3} + x^{2} - x + 2$ đạt cực đại tại điểm nào ?

Tính đạo hàm của hàm số $y = \log_{5} (x^{2} + 2) .$

Tìm giá trị lớn nhất của hàm số $y = x^{4} - 2 x^{2} - 15$ trên đoạn [-3;2]