Câu hỏi:

18/07/2020 424

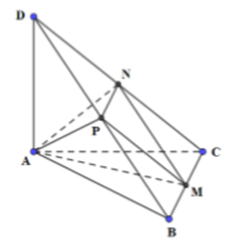
Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, $A B = 6 a, A C = 5 a, A D = 4 a .$ Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:

A. $V = \frac{5 a^{3}}{3} .$

B. $V = \frac{20 a^{3}}{3} .$

C. $V = 5 a^{3}$

D. $V = 10 a^{3}$

Xem lời giải

Câu hỏi trong đề: Tổng hợp 20 đề thi thử thpt quốc gia môn Toán cực hay có lời giải chi tiết !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn C.

Phương pháp:

+) Thể tích khối tứ diện OABC có OA, OB, OC đôi một vuông góc và có độ dài các cạnh đó lần lượt là a, b, c là: $V = \frac{1}{6} a b c$

Cách giải:

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong khai triển ${(a^{2} + \frac{1}{b})}^{7},$ số hạng thứ 5 là:

A. $- 35 a^{4} b$

B. $35 a^{4} b^{- 5}$

C. $- 35 a^{6} b^{- 4}$

D. $35 a^{6} b^{- 4}$

Lời giải

Chọn D.

Phương pháp:

Áp dụng Công thức khai triển nhị thức Newton:

Câu 2

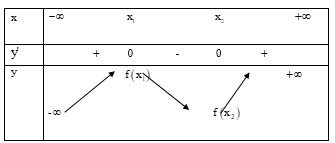
Cho hàm số $y = |x^{3} - m x + 1| .$ Gọi S là tập tất cả các số tự nhiên m sao cho hàm số đồng biến trên $[1; + \infty) .$ Tìm số phân tử của S.

A. 3

B. 10

C. 1

D. 9

Lời giải

Chọn A.

Cách giải:

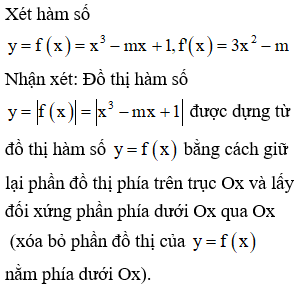
Câu 3

Nếu một hình chóp đều có chiều cao và cạnh đáy cùng tăng lên 3 lần thì thể tích của nó tăng lên

A. 18 lần.

B. 54 lần.

C. 9 lần.

D. 27 lần.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tìm GTLN, GTNN của hàm số $y = 3 - 2 \cos^{2} 3 x .$

A. min y = 1, max y = 3

B. min y = 1, max y = 5

C. min y = 2, max y = 3

D. min y = -1, max y = 3.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho tứ diện đều S.ABC có cạnh bằng 1. Mặt phẳng (P) đi qua điểm S và trọng tâm G của tam giác ABC cắt các cạnh AB, AC lần lượt tại M, N. Tính thể tích nhỏ nhất $V_{m i n}$ của khối tứ diện SAMN.

A. $V_{\min} = \frac{\sqrt{2}}{27}$

B. $V_{\min} = \frac{4}{9}$

C. $V_{\min} = \frac{\sqrt{2}}{18}$

D. $V_{\min} = \frac{\sqrt{2}}{36}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho tứ diện ABCD. Gọi I là trung điểm của BC, M là điểm trên cạnh DC. Một mp $(α)$ qua M, song song BC và AI. Gọi P, Q lần lượt là giao điểm của $(α)$ với BD và AD. Xét các mệnh đề sau:
(1) MP // BC (2) MQ // AC (3) PQ // AI (4) (MPQ) // (ABC)
Số mệnh đề đúng là:

A. 1

B. 3

C. 2

D. 4

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Tỉ lệ tăng dân số ở Việt Nam được duy trì ở mức 1,05%. Theo số liệu của Tổng cục thống kê, dân số Việt Nam năm 2014 có 90.728.900 người. Với tốc độ tăng dân số như thế thì vào năm 2030 thì dân số của Việt Nam là bao nhiêu?

A. 105.971.355 người.

B. 106.118.331 người.

C. 107.232.573 người.

D. 107.232.574 người

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, AB = 6a, AC = 5a, AD = 4a. Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:

Trong khai triển a2+1b7, số hạng thứ 5 là:

Cho hàm số y=x3−mx+1. Gọi S là tập tất cả các số tự nhiên m sao cho hàm số đồng biến trên 1;+∞. Tìm số phân tử của S.

Nếu một hình chóp đều có chiều cao và cạnh đáy cùng tăng lên 3 lần thì thể tích của nó tăng lên

Tìm GTLN, GTNN của hàm số y=3−2cos23x.

Cho tứ diện đều S.ABC có cạnh bằng 1. Mặt phẳng (P) đi qua điểm S và trọng tâm G của tam giác ABC cắt các cạnh AB, AC lần lượt tại M, N. Tính thể tích nhỏ nhất Vmin của khối tứ diện SAMN.

Tỉ lệ tăng dân số ở Việt Nam được duy trì ở mức 1,05%. Theo số liệu của Tổng cục thống kê, dân số Việt Nam năm 2014 có 90.728.900 người. Với tốc độ tăng dân số như thế thì vào năm 2030 thì dân số của Việt Nam là bao nhiêu?

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho tứ diện ABCD có các cạnh AB, AC và AD đôi một vuông góc với nhau, $A B = 6 a, A C = 5 a, A D = 4 a .$ Gọi M, N, P tương ứng là trung điểm của các cạnh BC, CD, DB. Thể tích V của tứ diện AMNP là:

Trong khai triển ${(a^{2} + \frac{1}{b})}^{7},$ số hạng thứ 5 là:

Cho hàm số $y = |x^{3} - m x + 1| .$ Gọi S là tập tất cả các số tự nhiên m sao cho hàm số đồng biến trên $[1; + \infty) .$ Tìm số phân tử của S.

Tìm GTLN, GTNN của hàm số $y = 3 - 2 \cos^{2} 3 x .$

Cho tứ diện đều S.ABC có cạnh bằng 1. Mặt phẳng (P) đi qua điểm S và trọng tâm G của tam giác ABC cắt các cạnh AB, AC lần lượt tại M, N. Tính thể tích nhỏ nhất $V_{m i n}$ của khối tứ diện SAMN.