Cho khối chóp tứ giác S. ABCD. Mặt phẳng đi qua trọng tâm các tam giác SAB, SAC, SAD chia khối chóp này thành hai phần có thể tích là V₁ và V₂ (V₁ < V₂). Tính tỉ lệ V₁/V₂.
A. 8/27
B. 16/81
C. 8/19
D. 16/75
Câu hỏi trong đề: 80 câu trắc nghiệm Khối đa diện nâng cao !!
Quảng cáo
Trả lời:
Chọn C
Gọi G₁, G₂, G₃ lần lượt là trọng tâm các tam giác SAB, SAD, SAC.
Gọi I, J lần lượt là trung điểm của AB, AC thì
Qua G₁ dựng đường song song với AB, cắt SA, SB lần lượt tại M, N.
Qua N dựng đường song song với BC, cắt SC tại P.
Qua P dựng đường song song với CD, cắt SD tại Q.
=> Thiết diện của hình chóp S. ABCD khi cắt bới (G₁G₂G₃) là tứ giác MNPQ.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn C
Gọi M là trung điểm của BC
=> AM BC (1)
Ta có
Mặt khác
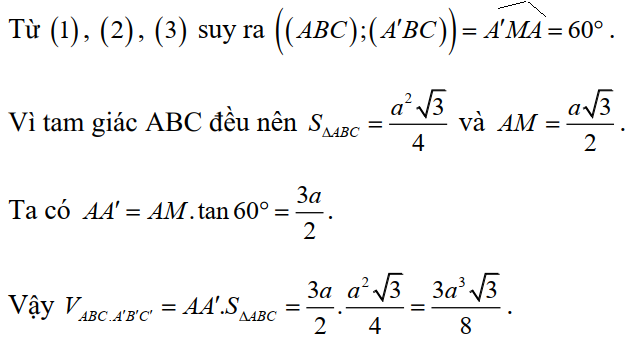
Lời giải
Chọn C
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.