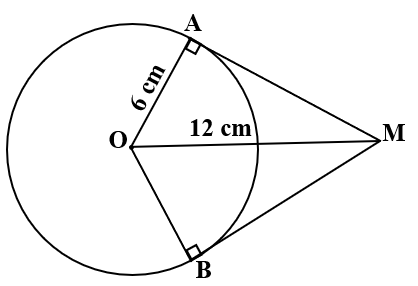
Cho đường tròn (O; 6cm) . Gọi A là điểm nằm ngoài đường tròn sao cho OA = 10cm.
Qua A dựng hai tiếp tuyến AM và AN đến (O), với M và N là tiếp điểm. Gọi giao điểm của AO và MN là H. Tìm khẳng định đúng?
A. OH = 3,6cm
B. AH = 4,8cm
C. MH = 6,4 cm
D.Tất cả sai
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án A
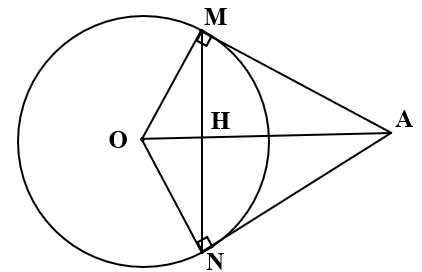
Theo tính chất hai tiếp tuyến cắt nhau ta có: OH là đường phân giác của góc MON
Tam giác MON có OM = ON (= R) nên đây là tam giác cân tại O có OH là đường phân giác nên đồng thời là đường cao.
Xét tam giác AMO vuông tại M có MH là đường cao.Áp dụng hệ thức cạnh và góc trong tam giác vuông ta có:
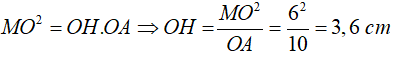
+) AH = AO – OH = 10 – 3,6 = 6,4 cm
+) = OH.AH = 3,6.6,4 = 23,04 ⇒ MH = 4,8cm
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án C
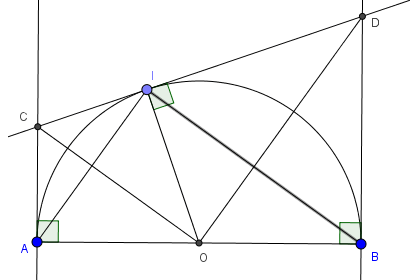
Câu 2
A. AC + BD = CD
B. AC . BD =
C. = DB. (AC + DB)
D. Có 2 khẳng định sai
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án D
* Do AC và CI là 2 tiếp tuyến cắt nhau tại C nên: CA = CI ( tính chất 2 tiếp tuyến cắt nhau)
* Do BD và DI là 2 tiếp tuyến cắt nhau tại D nên: DB = DI ( tính chất 2 tiếp tuyến cắt nhau).
Suy ra: AC + BD = CI + DI = CD. - A đúng
+) AC.BD = CI.DI (1)
Xét tam giác COD vuông tại O có đường cao OI nên:
CI.ID = = (2)
Từ (1) và (2) suy ra: AC.BD = - B đúng
Và = DI.DC = DB . (AC + BD) - C đúng
Vậy không có khẳng định nào là sai.
Câu 3
A. AB
B. 2AB
C. AC
D. 3AC
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Tam giác vuông
B. Tam giác đều
C. Tam giác cân
D. Tam giác tù
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. BD // OA
B. BD // AC
C. BD ⊥ OA
D. BD cắt OA
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập