Tìm tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức w=1+i3z+2, trong đó z-1≤2. A. Hình tròn tâm I3;3 bán kính R=4. B. Đường tròn tâm I3;3 bán kính R=4. C. Hình tròn tâm I3;3 bán kính R=...

Đáp án A.Cách 1: w=1+i3z+2⇔z=w−21+i3. Từ đóz−1≤2⇔w−21+i3−1≤2⇔w−3−i3≤21+i3⇔w−3+i3≤4 Vậy tập hợp cần tìm là hình tròn tâm I3;3 bán kính R=4. Chọn đáp án A.Cách 2: Gọi w=x+yi;x,y∈ℝ. Khi đó ta ców=1+i3z+2⇔x+yi=1+i3z+2⇔x−2+yi1+i3=z ⇒z−1=x−2+yi1+i3−1=x−3−y−3i1+i3⇒z−1=x−y3+iy−x3+434 z−1≤2⇒x−y32+y−x3+432≤8⇒x−32+y−32≤16.Vậy tập hợp cần tìm là hình tròn tâm I3;3 bán kính R=4. Chọn đáp án A.Bài toán tổng quát: Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số w=αz+β trong đó z là số phức tùy ý thỏa mãn z−z0≤R (z0,α≠0, β là những số phức cho trước, R là số thực dương cho trước).Tương tự như lời giải trên, ta có tập hợp cần tìm là hình tròn có tâm là điểm biểu diễn số phức αz0+β, với bán kính bằng Rα.

Câu hỏi:

24/11/2020 244

Tìm tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức $w = (1 + i \sqrt{3}) z + 2$ , trong đó $|z - 1| \leq 2$ .

A. Hình tròn tâm $I (3; \sqrt{3})$ bán kính $R = 4$ .

B. Đường tròn tâm $I (3; \sqrt{3})$ bán kính $R = 4$ .

C. Hình tròn tâm $I (3; \sqrt{3})$ bán kính $R = 8$ .

D. Đường tròn tâm $I (3; \sqrt{3})$ bán kính $R = 8$ .

Xem lời giải

Câu hỏi trong đề: Tổng hợp đề thi thptqg môn Toán hay nhất !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án A.

Cách 1: $w = (1 + i \sqrt{3}) z + 2 \Leftrightarrow z = \frac{w - 2}{1 + i \sqrt{3}}$ . Từ đó

$|z - 1| \leq 2 \Leftrightarrow |\frac{w - 2}{1 + i \sqrt{3}} - 1| \leq 2 \Leftrightarrow |w - 3 - i \sqrt{3}| \leq 2 |1 + i \sqrt{3}| \Leftrightarrow |w - (3 + i \sqrt{3})| \leq 4$

Vậy tập hợp cần tìm là hình tròn tâm $I (3; \sqrt{3})$ bán kính $R = 4$ . Chọn đáp án A.

Cách 2: Gọi $w = x + y i; (x, y \in ℝ)$ . Khi đó ta có

$w = (1 + i \sqrt{3}) z + 2 \Leftrightarrow x + y i = (1 + i \sqrt{3}) z + 2 \Leftrightarrow \frac{x - 2 + y i}{1 + i \sqrt{3}} = z$

$\Rightarrow |z - 1| = |\frac{x - 2 + y i}{1 + i \sqrt{3}} - 1| = |\frac{x - 3 - (y - \sqrt{3}) i}{1 + i \sqrt{3}}| \Rightarrow |z - 1| = |\frac{x - y \sqrt{3} + i (y - x \sqrt{3} + 4 \sqrt{3})}{4}|$

$|z - 1| \leq 2 \Rightarrow \sqrt{{(x - y \sqrt{3})}^{2} + {(y - x \sqrt{3} + 4 \sqrt{3})}^{2}} \leq 8 \Rightarrow {(x - 3)}^{2} + {(y - \sqrt{3})}^{2} \leq 16$ .

Vậy tập hợp cần tìm là hình tròn tâm $I (3; \sqrt{3})$ bán kính $R = 4$ . Chọn đáp án A.

Bài toán tổng quát: Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số $w = α z + β$ trong đó z là số phức tùy ý thỏa mãn $|z - z_{0}| \leq R$ ( $z_{0}, α \neq 0$ , $β$ là những số phức cho trước, R là số thực dương cho trước).

Tương tự như lời giải trên, ta có tập hợp cần tìm là hình tròn có tâm là điểm biểu diễn số phức $α z_{0} + β$ , với bán kính bằng $R |α|$ .

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Giả sử hàm chỉ mức mức sản xuất của một hãng DVD trong một ngày là $q (m, n) = m^{\frac{2}{3}} n^{\frac{1}{3}}$ , trong đó m là số lượng nhân viên và n là số lượng lao động chính. Mỗi ngày hãng phải sản xuất được ít nhất 40 sản phẩm để đáp ứng nhu cầu của khách hàng. Biết rằng tiền lương một ngày cho một nhân viên là 16 USD và cho một lao động chính là 27 USD. Tìm giá trị nhỏ nhất của chi phí trong một ngày của hãng sản xuất này.

A. 1446 USD

B. 1440 USD

C. 1908 USD

D. 1892 USD

Lời giải

Đáp án B.

Câu 2

Mệnh đề nào dưới đây đúng?

A. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b vuông góc với đường thẳng c thì a vuông góc với c.

B. Nếu đường thẳng a vuông góc với đường thẳng b và đường thẳng b song song với đường thẳng c thì a vuông góc với c.

C. Cho ba đường thẳng a, b, c vuông góc với nhau từng đôi một. Nếu có một đường thẳng d vuông góc với a thì d song song với b hoặc c.

D. Cho hai đường thẳng a và b song song với nhau. Một đường thẳng c vuông góc với a thì c vuông góc với mọi đường thẳng nằm trong mặt phẳng (a;b).

Lời giải

Đáp án B.

- A sai vì có thể xảy ra khả năng a và c song song với nhau và cùng vuông góc với b.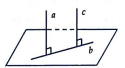

- C sai. Xét trường hợp a, b, c vuông góc với nhau từng đôi một và đồng quy tại một điểm. Khi đó $a ⊥ (b, c)$ . Do đó a vuông góc với mọi đường thẳng d nằm trong mặt phẳng (b;c), trong đó có những đường thẳng cắt cả b và c.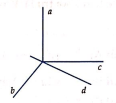

- D sai vì nếu c nằm trong (a;b) và vuông góc với a thì c không thể vuông góc với mọi đường thẳng nằm trong (a;b).

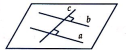
Vậy B đúng (dựa vào định nghĩa góc giữa hai đường thẳng trong không gian có thể thấy B đúng).

Câu 3

Mệnh đề nào dưới đây sai?

A. Hai khối chóp có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau

B. Hai khối hộp chữ nhật có diện tích toàn phần bằng nhau thì có thể tích bằng nhau

C. Hai khối lăng trụ có diện tích đáy và chiều cao tương ứng bằng nhau thì có thể tích bằng nhau

D. Hai khối lập phương có diện tích toàn phần bằng nhau thì có thể tích bằng nhau

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hàm số $y = f (x)$ có đồ thị là đường gấp khúc như hình vẽ bên. Tính $\int_{0}^{9} f (x) d x$ .

A. 18

B. 2

C. 0

D. 16

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một hình hộp chữ nhật có kích thước $4 \times 4 \times h$ chứa một khối cầu bán kính bằng 2 và tám khối cầu nhỏ hơn có bán kính bằng 1. Các khối cầu nhỏ đôi một tiếp xúc nhau và tiếp xúc với ba mặt của hình hộp, khối cầu lớn tiếp xúc với cả tám khối cầu nhỏ (xem hình vẽ). Tìm giá trị của h.

A. $2 + 2 \sqrt{7}$

B. $3 + 2 \sqrt{5}$

C. $4 + 2 \sqrt{7}$

D. $5 + 2 \sqrt{5}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Mệnh đề nào dưới đây sai?

A. Nếu hai mặt phẳng có một điểm chung thì chúng còn có vô số điểm chung khác nữa.

B. Nếu hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì chúng song song với nhau.

C. Nếu hai đường thẳng phân biệt cùng song song với một mặt phẳng thì song song với nhau.

D. Nếu một đường thẳng cắt một trong hai mặt phẳng song song với nhau thì sẽ cắt mặt phẳng còn lại.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong các dãy số có số hạng tổng quát dưới đây, dãy số nào là dãy giảm?

A. $u_{n} = \frac{n - 1}{n + 1}$

B. $v_{n} = \frac{2 n + 1}{5 n + 2}$

C. $w_{n} = \frac{3 n - 1}{n + 2}$

D. $t_{n} = \frac{3 n + 1}{5 n + 3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Tìm tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức w=1+i3z+2, trong đó z-1≤2.

Mệnh đề nào dưới đây đúng?

Mệnh đề nào dưới đây sai?

Cho hàm số y=fx có đồ thị là đường gấp khúc như hình vẽ bên. Tính ∫09fxdx.

Mệnh đề nào dưới đây sai?

Trong các dãy số có số hạng tổng quát dưới đây, dãy số nào là dãy giảm?

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Tìm tập hợp các điểm M trên mặt phẳng tọa độ biểu diễn các số phức $w = (1 + i \sqrt{3}) z + 2$ , trong đó $|z - 1| \leq 2$ .

Cho hàm số $y = f (x)$ có đồ thị là đường gấp khúc như hình vẽ bên. Tính $\int_{0}^{9} f (x) d x$ .