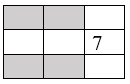
Cho bảng 3 x 3 ô vuông.

a) Viết 9 số nguyên khác 0 vào 9 ô của bảng. Biết rằng tích các số ở mỗi dòng đều là số nguyên âm. Chứng tỏ rằng luôn tồn tại một cột mà tích các số ở cột ấy là số nguyên âm.

b) Có thể điền được hay không 9 số nguyên vào 9 ô của bảng sao cho tổng các số ở ba dòng lần lượt bằng -15; -18; 78 và tổng các số ở ba cột lần lượt bằng 24; -12; 65?

Nếu n chia cho 3 dư 1 thì n có dạng n = 3k + 1. Khi đó n + 2 = 3k + 3 = 3(k+1) chia hết cho 3 nên n(n + 1)(n + 2) chia hết cho 3.

Nếu n chia cho 3 dư 2 thì n có dạng n = 3k + 2. Khi đó n + 1 = 3k + 2 + 1 = 3k + 3 = 3(k + 1) chia hết cho 3 nên n(n + 1)(n + 2) chia hết cho 3.

Suy ra n(n + 1)(n + 2) chia hết cho 3 với mọi số nguyên n.

Vậy n(n + 1)(n + 2) chia hết cho 2 và 3 với mọi số nguyên n.

b)

+) Nếu n chẵn thì n chia hết cho 2 thì n + 2 chia hết cho 4 nên n(n + 1)(n + 2)(n + 3) chia hết cho 8.

Nếu n lẻ thì n + 1 chia hết cho 2 thì n + 3 chia hết cho 4 nên n(n + 1)(n + 2)(n +3) chia hết cho 8.

Suy ra n(n + 1)(n + 2)(n +3) chia hết cho 8 với mọi số nguyên n.

+) Nếu n chia hết cho 3 thì n(n + 1)(n + 2)(n + 3) chia hết cho 3.

Nếu n chia cho 3 dư 1 thì n có dạng n = 3k + 1. Khi đó n + 2 = 3k + 3 = 3(k+1) chia hết cho 3 nên n(n + 1)(n + 2)(n + 3) chia hết cho 3.

Nếu n chia cho 3 dư 2 thì n có dạng n = 3k + 2. Khi đó n + 1 = 3k + 2 + 1 = 3k + 3 = 3(k + 1) chia hết cho 3 nên n(n + 1)(n + 2)(n + 3) chia hết cho 3.

Suy ra n(n + 1)(n + 2)(n + 3) chia hết cho 3 với mọi số nguyên n.

Vậy n(n + 1)(n + 2)(n + 3) chia hết cho 2 và 3 với mọi số nguyên n.