Câu hỏi:
25/04/2022 2,002Có bao nhiêu giá trị nguyên \(m\) để hàm số \(y = {x^3} - 3{x^2} - mx + 4\) có hai điểm cực trị thuộc khoảng \(\left( { - 3;3} \right)?\)
Đáp án chính xác
Câu hỏi trong đề:
[Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!
Sách mới 2k7: Bộ 20 đề minh họa Toán, Lí, Hóa, Văn, Sử, Địa…. form chuẩn 2025 của Bộ giáo dục (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có \(y = {x^3} - 3{x^2} - mx + 4{\rm{ }}\left( 1 \right)\)
\(y' = 3{x^2} - 6x - m\)
Xét: \(g\left( x \right) = 3{x^2} - 6x - m\)
Hàm số \(\left( 1 \right)\) có hai cực trị thuộc khoảng \(\left( { - 3;3} \right)\) khi \(g\left( x \right) = 0\) có hai nghiệm phân biệt thuộc khoảng \(\left( { - 3;3} \right).\)
Ta có: \(g\left( x \right) = 0 \Leftrightarrow 3{x^2} - 6x - m = 0 \Leftrightarrow 3{x^2} - 6x = m\)
Xét: \(h\left( x \right) = 3{x^2} - 6x \Rightarrow h'\left( x \right) = 6x - 6,\) cho \(h'\left( x \right) = 0 \Leftrightarrow x = 1.\)
Bảng biến thiên:
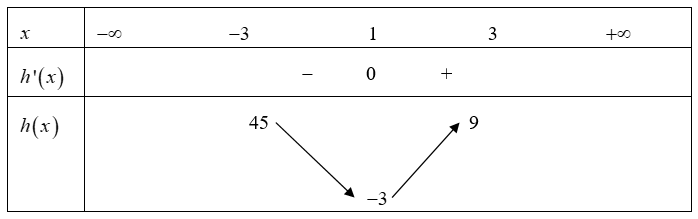
Dựa vào bảng biến thiên, ta có \(m \in \left( { - 3;9} \right).\) Vậy có 11 giá trị nguyên của \(m.\)
Đáp án D
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm tất cả các giá trị của \(m\) để hàm số \(y = \left( {m - 1} \right){x^3} - 3\left( {m - 1} \right){x^2} + 3x + 2\) đồng biến trên \(\mathbb{R}.\)
Xem đáp án »
25/04/2022
25,744
Câu 2:
Cho biểu thức \(P = \sqrt[4]{{x\sqrt[3]{{{x^2}.\sqrt[3]{x}}}}},x >0.\) Mệnh đề nào dưới đây là đúng?
Xem đáp án »
25/04/2022
8,726
Câu 3:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R},\) có \(f'\left( x \right) = {\left( {x + 2} \right)^2}{\left( {x - 2} \right)^3}\left( { - x + 5} \right).\) Số điểm cực trị của hàm số \(y = f\left( x \right)\) là
Xem đáp án »
25/04/2022
4,860
Câu 4:
Cho hàm số \(f\left( x \right)\) có đại hàm \(f'\left( x \right) = {\left( {x + 1} \right)^2}\left( {{x^2} - 4x} \right)\). Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = f\left( {2{x^2} - 12x + m} \right)\) có đúng 5 điểm cực trị?
Xem đáp án »
25/04/2022
4,316
Câu 5:
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật có \(AB = a;BC = 2a.\) Hai mặt phẳng \(\left( {SAB} \right)\) và mặt phẳng \(\left( {SAD} \right)\) cùng vuông góc với mặt phẳng đáy, cạnh \(SC\) hợp với mặt đáy góc \({60^0}.\) Tính thể tích khối chóp \(S.ABCD\) theo \(a.\)
Xem đáp án »
25/04/2022
2,812
Câu 6:
Cho hình chóp \(S.ABCD\) có đáy là hình thang có \(AD//BC,M\) là điểm di động trong hình thang \(ABCD.\) Qua \(M\) kẻ đường thẳng song song với \(SA\) và \(SB\) lần lượt cắt các mặt \(\left( {SBC} \right)\) và \(\left( {SAD} \right)\) tại \(N\) và \(P.\) Cho \(SA = a,SB = b.\) Tìm giá trị lớn nhất của biểu thức \(T = M{N^2}.MP.\)
Xem đáp án »
25/04/2022
2,588
Câu 7:
Cho \(a,b,c\) là các số thực khác 0 thỏa mãn \({4^a} = {25^b} = {10^c}.\) Tính giá trị biểu thức \(A = \frac{c}{a} + \frac{c}{b}.\)
Xem đáp án »
25/04/2022
2,570
Bình luận
🔥 Đề thi HOT:
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 3)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 5)
-
30 đề thi THPT Quốc gia môn Toán năm 2022 có lời giải (đề 1)
-
Đề minh họa THPT Quốc gia môn Toán năm 2023 có đáp án
về câu hỏi!