Với mức tiêu thụ thức ăn của một trang trại \[A\] không đổi như dự định thì lượng thức ăn dự trữ đủ dùng cho \(100\) ngày. Nhưng thực tế, kể từ ngày thứ hai trở đi lượng thức ăn của trang trại đã tăng thêm \(4\% \) so với ngày trước đó. Hỏi lượng thức ăn mà trang trại \[A\] đã dự trữ đủ dùng cho bao nhiêu ngày ?

Chọn đáp án A

Hàm số \(y = {\log _3}\left( {x - 1} \right)\) có nghĩa khi \(x - 1 >0 \Rightarrow x >1\).

Vậy tập xác định của hàm số \(y = {\log _3}\left( {x - 1} \right)\) là \(\left( {1; + \infty } \right)\).

Chọn đáp án D

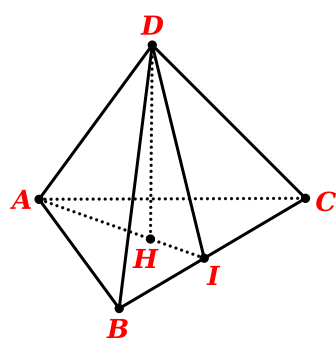
Gọi tứ diện \[ABCD\] là tứ diện đều cạnh a.

Gọi \[H\] là tâm của tam giác\[ABC\]. Khi đó \(DH \bot \left( {ABC} \right)\) tại \[H\].

Gọi \(I\) là trung điểm của \[BC\]. Khi đó góc giữa mặt phẳng \(\left( {DBC} \right)\) và \(\left( {ABC} \right)\) là góc \(\widehat {DIH}\)

Ta có \(\cos \widehat {\left( {\left( {ABC} \right),\left( {DBC} \right)} \right)} = \cos \widehat {DIH} = \frac{{IH}}{{ID}}\).

Tam giác \[ABC\] đều \( \Rightarrow IH = \frac{1}{3}IA = \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}\).

Tam giác \[DBC\] đều \( \Rightarrow ID = \frac{{a\sqrt 3 }}{2} \Rightarrow \cos \widehat {\left( {\left( {ABC} \right),DBC} \right)} = \frac{1}{3}\).