Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (đề 2)
26 người thi tuần này 4.6 23.8 K lượt thi 50 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Thị Minh Khai (Hà Nội) lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Liên trường THPT (Nghệ An) có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên Đại học Vinh lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Cụm liên trường Nghệ An có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Bắc Ninh có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Chuyên ĐH KHTN Hà Nội lần 1 có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 Sở Hưng Yên có đáp án
Đề thi thử Tốt nghiệp THPT Toán 2025-2026 THPT Nguyễn Gia Thiều (Hà Nội) có đáp án
Danh sách câu hỏi:
Lời giải
Chọn đáp án C
Tổng số học sinh của lớp là \(18 + 17 = 35\).
Số cách chọn 1 học sinh trong lớp là 35 cách.
Câu 2
A.4.
B. 3.
C. 9.
D.\(\frac{1}{4}\).
Lời giải
Chọn đáp án A
Ta có: \[{u_2} = {u_1}.q \Rightarrow q = \frac{{{u_2}}}{{{u_1}}} = \frac{{12}}{3}\, = \,4\].
Câu 3
A. \(\left( {\frac{1}{2};2} \right)\).
B. \(\left( {2;4} \right)\).
C.\(\left( { - 1;0} \right)\).
D. \(\left( {3;6} \right)\).
Lời giải
Chọn đáp án A
\({4^x} - {3.2^x} + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}{2^x} = 1\\{2^x} = 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1 \in \left( {\frac{1}{2};2} \right)\end{array} \right.\).
Câu 4
A.\(\frac{{2{a^3}\sqrt 3 }}{3}\).
B.\(\frac{{2{a^3}\sqrt 3 }}{2}\).
C.\(\frac{{2{a^3}}}{3}\).
D.\(\frac{{5{a^3}}}{{\sqrt 3 }}\).
Lời giải
Chọn đáp án A
Thể tích khối chóp là \(V = \frac{1}{3}.a.2{a^2}\sqrt 3 = \frac{{2{a^3}\sqrt 3 }}{3}\).
Câu 5
A. \(\left( {1; + \infty } \right)\).
B. \(\left[ {1; + \infty } \right)\).
C. \(\left( { - \infty ;1} \right)\).
D.\(\left( {3; + \infty } \right)\).
Lời giải
Chọn đáp án A
Hàm số \(y = {\log _3}\left( {x - 1} \right)\) có nghĩa khi \(x - 1 >0 \Rightarrow x >1\).
Vậy tập xác định của hàm số \(y = {\log _3}\left( {x - 1} \right)\) là \(\left( {1; + \infty } \right)\).
Câu 6
A. \[F'\left( x \right) = - f\left( x \right)\], \[\forall x \in K\].
B. \[g'\left( x \right) = G\left( x \right)\], \[\forall x \in K\].
C. \[F'\left( x \right) + G'\left( x \right) = f\left( x \right) - g\left( x \right)\], \[\forall x \in K\].
D. \[F'\left( x \right) + G'\left( x \right) = f\left( x \right) + g\left( x \right)\], \[\forall x \in K\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(8\).
B. \(24\).
C. \(12\).
D. \(72\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A.\(R = a\).
B.\(R = a\sqrt 2 \).
C.\(R = a\sqrt 3 \).
D.\(R = 2a\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A.\(S = \pi {R^2}\).
B. \(V = \frac{4}{3}\pi {R^3}\).
C. \(S = 4\pi {R^2}\).
D. \(3V = S.R\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
A. \(\left( { - 1;\,\,0} \right)\).
B. \(\left( { - 1;\,\,1} \right)\).
C. \(\left( { - \infty ;\,\, - 1} \right)\).
D. \[8a + d\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
A.\(y' = \frac{{{7^x}}}{{\ln 7}}\) .
B.\(y' = {7^x}\ln 7\).
C.\(y' = x{.7^{x - 1}}\).
D.\(y' = {7^{x - 1}}\ln 7\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13
A. \(x = 3\).
B. \(x = 1\).
C. \(x = 2\).
D. \(x = - 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
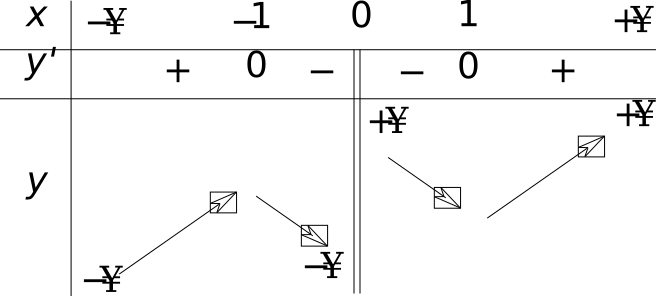
Câu 14
A. \(a >0;d >0\).
B. \(a < 0;d >0\).
C. \(a >0;d < 0\).
D. \(a < 0;d < 0.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15
A. \[y = 1\].
B. \[y = - 2\].
C. \[x = 1\].
D. \[x = - 2\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16
A. \[\left[ {4; + \infty } \right)\].
B. \[\left[ {2; + \infty } \right)\].
C. \[\left( {4; + \infty } \right)\].
D. \[\left( { - \infty ;4} \right]\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17
A. \(6\).
B. \(5\).
C. \(3\).
D. \(4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. 3.
B. 2.
C. 1.
D. 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. \(\left( {4;3} \right)\).
B. \(\left( { - 4;3} \right)\).
C. \(\left( {4; - 3} \right)\).
D. \(\left( { - 4; - 3} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20
A. \(\overline w = 3 - 7i\).
B. \(\overline w = 7 - 3i\).
C. \(\overline w = 7 + 3i\).
D. \(\overline w = 4 - i\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 21
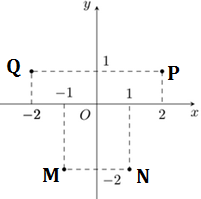
A. \(M\left( { - 1\,;\,0} \right)\).
B. \(N\left( {0\,;\, - 1} \right)\).
C. \(P\left( {1\,;\,0} \right)\).
D. \(Q\left( {0;\,1} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 22
A. \(\left( {1\,;\,0\,;\,0} \right)\).
B. \(\left( {3\,;\, - 1\,;\,0} \right)\).
C. \(\left( {3\,;\,0\,;\,2} \right)\).
D. \(\left( {0\,;\, - 1\,;\,2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 23
A.\(I\left( {1;2;3} \right);R = 3\).
B.\(I\left( { - 1;2; - 3} \right);R = 3\).
C.\(I\left( {1; - 2;3} \right);R = 3\).
D.\(I\left( {1;2; - 3} \right);R = 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 24
A.\(x + 2z = 0\).
B. \(x - 2z = 0\).
C. \(y - z - 2 = 0\).
D.\(y + z = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 25
A. Song song.
B. Chéo nhau.
C. Cắt nhau.
D. Trùng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 26
A. \(\frac{{\sqrt 3 }}{2}\).
B. \(\frac{{\sqrt 2 }}{2}\).
C. \(\frac{1}{2}\).
D. \(\frac{1}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 27
A. \(2\).
B. \(3\).
C. \(1\).
D. \(4\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 28
A. \[20\].
B. \[13\].
C. \[ - 3\].
D. \[ - 7\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 29
A. \[a = {b^5}\].
B. \[{a^5} = {b^3}\].
C. \[{a^5}.b = 1\].
D. \[{a^5}.{b^3} = 1\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
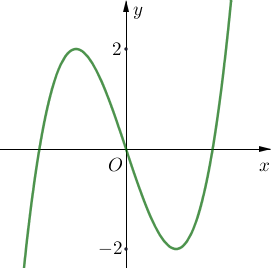
Câu 30
A. \(y = - {x^3} + 3{x^2} - 2.\)
B. \(y = {x^3} - 6{x^2} + 9x + 2.\)
C. \(y = {x^3} - 3{x^2} - 2.\)
D. \(y = {x^3} - 6{x^2} + 9x - 2.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 31
A. \(\left( { - \infty ;\frac{1}{2}} \right] \cup \left[ {16; + \infty } \right)\).
B. \(\left( { - \infty ;\frac{1}{2}} \right) \cup \left( {16; + \infty } \right)\).
C. \(\left( {0;\frac{1}{2}} \right] \cup \left[ {16; + \infty } \right)\).
D. \(\left( {0;\frac{1}{2}} \right) \cup \left( {16; + \infty } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 32
A. \(4\pi {a^2}\).
B. \(\pi {a^2}\sqrt 2 \).
C. \(8\pi {a^2}\).
D. \(4\pi {a^2}\sqrt 2 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 33
A. \(I = 4\).
B. \(I = - 4\).
C. \(I = - 2\).
D. \(I = 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 34
A.\(S = \pi \int\limits_0^2 {\left( {2{x^2} - 2} \right){\rm{d}}x} \).
B.\(S = 2\int\limits_0^2 {\left| {{x^2} - 1} \right|{\rm{d}}x} \).
C.\(S = \int\limits_0^2 {\left( {2{x^2} - 2} \right){\rm{d}}x} \).
D.\(S = 2\pi \int\limits_0^2 {\left| {{x^2} - 1} \right|{\rm{d}}x} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 36
A. \(6\).
B. \(\sqrt 2 \).
C. \(4\).
D. \(\sqrt 6 \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 37
A. \(3x + y + z - 6 = 0\).
B. \(6x - 2y - 2z - 1 = 0\).
C. \(3x - y - z + 1 = 0\).
D. \(3x - y - z = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 38
A.\(\left\{ \begin{array}{l}x = t\\y = 1 + 3t\\z = 2 - 2t\end{array} \right.\).
B.\(\left\{ \begin{array}{l}x = 1\\y = 3 - 3t\\z = - 2 + 6t\end{array} \right.\).
C.\(\left\{ \begin{array}{l}x = 1\\y = 3 + 2t\\z = - 2 + t\end{array} \right.\).
D.\(\left\{ \begin{array}{l}x = 1\\y = 3 + t\\z = - 2 + 2t\end{array} \right.\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 39
A. \(\frac{1}{{247}}\) .
B. \(\frac{1}{{481}}\).
C. \(\frac{{18}}{{9139}}\).
D. \(\frac{1}{{5928}}\) .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 40
A. \(\frac{{a\sqrt {210} }}{{70}}\).
B. \(\frac{{2a\sqrt {210} }}{{35}}\).
C. \(\frac{{3a\sqrt {210} }}{{35}}\).
D. \(\frac{{a\sqrt {210} }}{{35}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 42
A. \(39\) (ngày).
B. \(40\) (ngày).
C. \(41\) (ngày).
D. \(42\) (ngày).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 44
A. \(169\pi {a^3}\).
B. \(52\pi {a^3}\).
C.\(104\pi {a^3}\).
D. \(\frac{{104\pi {a^3}}}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 45
A.\(506\).
B.\(\frac{{1009}}{2}\).
C.\(\frac{{2019}}{2}\).
D.\[505\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 47
A. \[\left( {13;15} \right)\].
B. \[\left( { - 15, - 13} \right)\].
C. \[\left( {4;6} \right)\].
D. \[\left( { - 6; - 4} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 48
A. \[2020\].
B. \[P = 2018\].
C. \[P = 2019\].
D. \[P = 2021\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 49
A. \(V = \frac{{9\sqrt 2 {a^3}}}{{320}}\).
B. \(V = \frac{{3\sqrt 2 {a^3}}}{{320}}\).
C. \(V = \frac{{\sqrt 2 {a^3}}}{{96}}\).
D. \(V = \frac{{3\sqrt 2 {a^3}}}{{80}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 50
A. \(2018.\)
B. \(2019.\)
C. \(2020.\)
D. \(2021.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.