Câu hỏi:
14/04/2022 416Cho hàm số \(y = f\left( x \right) >0\) xác định, có đạo hàm trên đoạn \(\left[ {0;1} \right]\) và thỏa mãn: \(g\left( x \right) = 1 + 2020\int\limits_0^x {f\left( t \right){\rm{dt}}} \), \(g\left( x \right) = {f^2}\left( x \right)\). Tính \(\int\limits_0^1 {\sqrt {g\left( x \right)} {\rm{d}}x} \).
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có \(g\left( x \right) = 1 + 2020\int\limits_0^x {f\left( t \right){\rm{dt}}} \)\( \Rightarrow g'\left( x \right) = 2020f\left( x \right) = 2020\sqrt {g\left( x \right)} \)
\( \Rightarrow \frac{{g'\left( x \right)}}{{\sqrt {g\left( x \right)} }} = 2020\)\( \Rightarrow \int\limits_0^t {\frac{{g'\left( x \right)}}{{\sqrt {g\left( x \right)} }}{\rm{d}}x = 2020} \int\limits_0^t {{\rm{d}}x} \)\( \Rightarrow \left. {2\left( {\sqrt {g\left( x \right)} } \right)} \right|_0^t = \left. {2020x} \right|_0^t\)
\( \Rightarrow 2\left( {\sqrt {g\left( t \right)} - 1} \right) = 2020t\) (do \(g\left( 0 \right) = 1\))
\( \Rightarrow \sqrt {g\left( t \right)} = 1010t + 1\)
\( \Rightarrow \int\limits_0^1 {\sqrt {g\left( t \right)} {\rm{dt}}} = \left. {\left( {505{t^2} + t} \right)} \right|_0^1 = 506\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn đáp án A
Hàm số \(y = {\log _3}\left( {x - 1} \right)\) có nghĩa khi \(x - 1 >0 \Rightarrow x >1\).
Vậy tập xác định của hàm số \(y = {\log _3}\left( {x - 1} \right)\) là \(\left( {1; + \infty } \right)\).
Lời giải
Chọn đáp án D
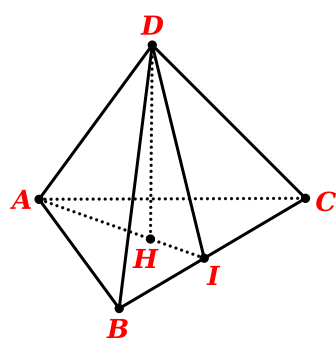
Gọi tứ diện \[ABCD\] là tứ diện đều cạnh a.
Gọi \[H\] là tâm của tam giác\[ABC\]. Khi đó \(DH \bot \left( {ABC} \right)\) tại \[H\].
Gọi \(I\) là trung điểm của \[BC\]. Khi đó góc giữa mặt phẳng \(\left( {DBC} \right)\) và \(\left( {ABC} \right)\) là góc \(\widehat {DIH}\)
Ta có \(\cos \widehat {\left( {\left( {ABC} \right),\left( {DBC} \right)} \right)} = \cos \widehat {DIH} = \frac{{IH}}{{ID}}\).
Tam giác \[ABC\] đều \( \Rightarrow IH = \frac{1}{3}IA = \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}\).
Tam giác \[DBC\] đều \( \Rightarrow ID = \frac{{a\sqrt 3 }}{2} \Rightarrow \cos \widehat {\left( {\left( {ABC} \right),DBC} \right)} = \frac{1}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải