Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (đề 23)

12133 lượt thi
50 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Trong không gian Oxyz, cho mặt phẳng \[\left( P \right):2x - y + z + 4 = 0\]. Khi đó mặt phẳng (P) có một vectơ pháp tuyến là

A. \[\overrightarrow {{n_1}} = \left( {2; - 1;1} \right)\]

B. \[\overrightarrow {{n_2}} = \left( {2;1;1} \right)\]

C. \[\overrightarrow {{n_4}} = \left( { - 2;1;1} \right)\]

D. \[\overrightarrow {{n_3}} = \left( {2;1;4} \right)\]

Xem đáp án

Đáp án A

Phương pháp

Mặt phẳng \(\left( P \right):ax + by + cz + d = 0\) có một vectơ pháp tuyến \(\overrightarrow n = \left( {a;b;c} \right)\)

Cách giải

Mặt phẳng \(\left( P \right):2x - y + z + 4 = 0\) có một VTPT là \(\overrightarrow n = \left( {2; - 1;1} \right).\)

Câu 2:

Cho a là số thực dương bất kì khác 1. Tính \[S = {\log _a}\left( {{a^3}\sqrt[4]{a}} \right)\].

A. \[S = \frac{3}{4}\]

B. \[S = 7\]

C. \[S = \frac{{13}}{4}\]

D. \[S = 12\]

Xem đáp án

Đáp án C

Phương pháp

Sử dụng các công thức lũy thừa thu gọn biểu thức dưới dấu logarit và sử dụng công thức \({\log _a}{a^n} = n.\)

Cách giải

Ta có: \(S = {\log _a}\left( {{a^3}\sqrt[4]{a}} \right) = {\log _a}\left( {{a^3}.{a^{\frac{1}{4}}}} \right) = {\log _a}^{\frac{{13}}{4}} = \frac{{13}}{4}.\)

Câu 3:

Cho hàm số \[y = f\left( x \right)\] có đạo hàm liên tục trên \[\mathbb{R}\] và có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. \[\left( {1; + \infty } \right)\]

B. \[\left( { - 1;0} \right)\]

C. \[\left( { - \infty ;1} \right)\]

D. \[\left( {0;1} \right)\]

Xem đáp án

Đáp án D

Phương pháp

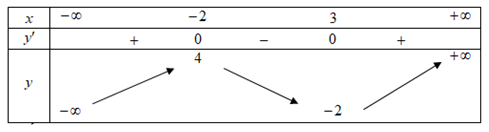
Sử dụng cách đọc bảng biến thiên để suy ra khoảng đồng biến của hàm số.

Hàm số liên tục trên \(\left( {a;b} \right)\) có \(y' > 0\) với \(x \in \left( {a;b} \right)\) thì hàm số đồng biến trên \(\left( {a;b} \right).\)

Cách giải

Từ BBT ta có hàm số đồng biến trên các khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right).\)

Câu 4:

Cho phương trình \[{2^{2x}} - {5.2^x} + 6 = 0\] có hai nghiệm \[{x_1},{x_2}\]. Tính \[P = {x_1}.{x_2}\].

A. \[P = {\log _2}6\]

B. \[P = 2{\log _2}3\]

C. \[P = {\log _2}3\]

D. \[P = 6\]

Xem đáp án

Đáp án C

Phương pháp

Coi phương trình đã cho là bậc hai ẩn \({2^x}\), giải phương trình tìm x và kết luận.

Cách giải

Ta có: \({2^{2x}} - {5.2^x} + 6 = 0 \Leftrightarrow \left( {{2^x} - 2} \right)\left( {{2^x} - 3} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}{2^x} = 2\\{2^x} = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = {\log _2}3\end{array} \right.\)

Do đó \(P = {x_1}{x_2} = 1.{\log _2}3 = {\log _2}3.\)

Câu 5:

Cho cấp số cộng có \[{u_1} = - 3;{u_{10}} = 24\]. Tìm công sai d?

A. \[d = \frac{7}{3}\]

B. \[d = - 3\]

C. \[d = - \frac{7}{3}\]

D. \[d = 3\]

Xem đáp án

Đáp án D

Phương pháp

Sử dụng công thức: Cho cấp số cộng có số hạng đầu \({u_1}\) và công sai d thì số hạng thứ \(n\left( {n > 1} \right)\) là

\({u_n} = {u_1} + \left( {n - 1} \right)d.\)

Từ đó ta tìm được công sai d.

Cách giải

Ta có \({u_{10}} = {u_1} + 9d \Leftrightarrow - 3 + 9d = 24 \Leftrightarrow 9d = 27 \Leftrightarrow d = 3.\)

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Bài thi liên quan:

Các bài thi hot trong chương:

Đánh giá trung bình

Thi Online Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề)