Một công ty cần xây dựng một cái kho chứa hàng dạng hình hộp chữ nhật (có nắp) bằng vật liệu gạch và xi măng có thể tích 2000 \[{m^3}\], đáy là hình chữ nhật có chiều dài bằng hai lần chiều rộng. Người ta cần tính toán sao cho chi phí xây dựng là thấp nhất, biết giá xây dựng là 500.000 đồng/\[{m^2}\]. Khi đó chi phí thấp nhất gần với số nào dưới đây?

A. 495969987.

B. 495279087.

C. 495288088.

D. 495289087.

Xem lời giải

Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án D

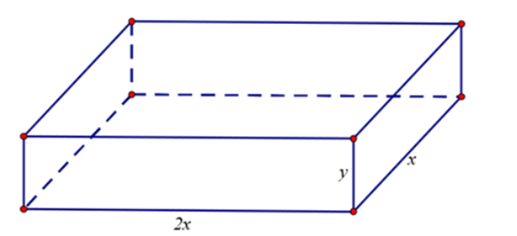
Một công ty cần xây dựng một cái kho chứa hàng dạng hình hộp chữ nhật (ảnh 1)

Gọi kích thước đáy của cái kho cần xây dựng là \(x\left( m \right)\) và \(2x\left( m \right),\) chiều cao của kho là \(y\left( m \right),\) (với \(x,y > 0\))

Ta có \(V = 2{x^2}y = 2000 \Rightarrow y = \frac{{1000}}{{{x^2}}}\left( m \right)\)

Diện tích toàn phần của hình hộp chữ nhật là

\({S_{tp}} = 2\left( {x.2x + x.y + 2x.y} \right) = 4{x^2} + 6xy = 4{x^2} + \frac{{6000}}{x}\)

\( = 4{x^2} + \frac{{3000}}{x} + \frac{{3000}}{x} \ge 3\sqrt[x]{{4{x^2}.\frac{{3000}}{x}.\frac{{3000}}{x}}} = 300\sqrt[3]{{36}}\left( {{m^2}} \right)\)

Dấu đẳng thức xảy ra khi và chỉ khi \(4{x^2} = \frac{{3000}}{x} \Leftrightarrow x = \sqrt[3]{{750}}\left( m \right)\)

Chi phí xây dựng thấp nhất khi đó sấp sỉ là \(300\sqrt[3]{{36}}.500000 \approx 495289087\) đồng

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Số các giá trị nguyên của m để hàm số \[f\left( x \right) = \frac{1}{3}{x^3} - \left( {m + 50} \right){x^2} + \left( {{m^2} + 100m} \right)x + 2020m\] nghịch biến trên \[\left( {7;13} \right)\] là

A. 95

B. 94

C. 96

D. Vô số

Lời giải

Đáp án A

Tập xác định: \(D = \mathbb{R}.\)

Ta có, \(f'\left( x \right) = {x^2} - 2\left( {m + 50} \right)x + {m^2} + 100m\)

Để hàm số nghịch biến trên \(\left( {7;13} \right)\) thì phương trình \(f'\left( x \right) = 0\) phải có hai nghiệm \({x_1},{x_2}\) thỏa mãn \(\left\{ \begin{array}{l}{x_1} \le 7\\{x_2} \ge 13\end{array} \right..\)

Từ đó, ta có hệ phương trình: \(\left\{ \begin{array}{l}\Delta ' = {\left[ { - \left( {m + 50} \right)} \right]^2} - \left( {{m^2} + 100m} \right) = 2500 > 0,\forall m\\{x_1} = m \le 7\\{x_2} = m + 100 \ge 13\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}m \le 7\\m \ge - 87\end{array} \right. \Leftrightarrow - 87 \le m \le 7\)

Do m nguyên, cho nên tập hợp các giá trị của m là: \(S = \left\{ { - 87; - 86;...;6;7} \right\}\)

Có 95 giá trị nguyên của m thỏa mãn.

Câu 2

Cho phương trình \[{\log _3}^2\left( {9x} \right) - \left( {m + 5} \right){\log _3}x + 3m - 10 = 0\]. Số giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt thuộc \[\left[ {1;81} \right]\] là

A. 2.

B. 3.

C. 4.

D. 5.

Lời giải

Đáp án C

+) Ta có \(\log _3^2\left( {9x} \right) - \left( {m + 5} \right){\log _3}x + 3m - 10 = 0.\) Đặt \(t = {\log _3}x.\) Vì \(x \in \left[ {1;81} \right]\) nên \(t \in \left[ {0;4} \right].\)

Khi đó phương trình đã cho trở thành: \({t^2} - \left( {m + 1} \right)t + 3m - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = m - 2\end{array} \right.\)

+) Ycbt \( \Leftrightarrow \left\{ \begin{array}{l}0 \le m - 2 \le 4\\m - 2 \ne 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2 \le m \le 6\\m \ne 5\end{array} \right..\) Vậy có 4 số nguyên m thỏa ycbt.

Câu 3