Câu hỏi:
28/06/2022 265Trong không gian tọa độ Oxyz, cho ba mặt phẳng (\[\left( {{P_1}} \right):\;2x + y + 2z - 5 = 0,\;\left( {{P_2}} \right):\;2x + y + 2z + 13 = 0,\] \[\left( Q \right):\;2x - 2y - z - 5 = 0,\] và điểm \[A\left( { - 2;0;0} \right)\] nằm giữa hai mặt phẳng \[\left( {{P_1}} \right),\;\left( {{P_2}} \right).\] Mặt cầu (S) có tâm \[I\left( {a;b;c} \right)\] luôn đi qua A và tiếp xúc với hai mặt phẳng \[\left( {{P_1}} \right),\;\left( {{P_2}} \right).\] Khi khối cầu \[\left( S \right)\] cắt mặt phẳng (Q) theo thiết diện là hình tròn có diện tích lớn nhất thì \[a + b - 2c\] bằng
Đáp án chính xác
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Mặt phẳng cách đều hai mặt phẳng \(\left( {{P_1}} \right),\left( {{P_2}} \right)\) có phương trình dạng \(\left( P \right):2x + y + 2z + D = 0\)
Lại có \(d\left( {{P_1};P} \right) = d\left( {{P_2};P} \right) \Leftrightarrow \frac{{\left| {D + 5} \right|}}{{\sqrt {4 + 1 + 4} }} = \frac{{\left| {D - 13} \right|}}{{\sqrt {4 + 1 + 4} }} \Leftrightarrow \left| {P + 5} \right| = \left| {P - 13} \right| \Leftrightarrow \left[ \begin{array}{l}{\rm{D}} + 5 = D - 13\\D + 5 = 13 - D\end{array} \right. \Leftrightarrow D = 4\)
Vậy \(\left( P \right):2x + y + 2z + 4 = 0.\) Tâm \(I \in \left( P \right)\) và điểm \(A \in \left( P \right)\)
Điểm I nằm trên giao tuyến của mặt cầu \(\left( {A;R} \right)\) với \(R = d\left( {{P_1};\left( P \right)} \right) = 3\) và mặt phẳng \(\left( P \right)\)
Mặt phẳng \(\left( P \right) \bot \left( Q \right)\), để \(\left( S \right)\) cắt mặt phẳng \(\left( Q \right)\) theo thiết diện là hình tròn có diện tích lớn nhất thì \(d{\left( {I;\left( Q \right)} \right)_{\min }}\)
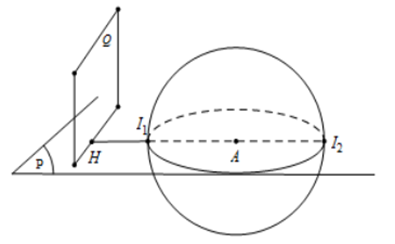
Để \(d{\left( {I;\left( Q \right)} \right)_{\min }}\) thì \(I = AH \cap \left( {A;R} \right),\) phương trình \(AH:\left\{ \begin{array}{l}x = - 2 + 2t\\y = - 2t\\z = - t\end{array} \right.\)
Gọi \(I\left( { - 2 + 2t; - 2t; - t} \right) \Rightarrow I{A^2} = 9{t^2} = 9 \Leftrightarrow t = \pm 1 \Rightarrow \left[ \begin{array}{l}I\left( {0; - 2; - 1} \right)\\I\left( { - 4;2;1} \right)\end{array} \right.\)
Kiểm tra khoảng cách từ I đến \(\left( Q \right)\) suy ra \(I\left( {0; - 2; - 1} \right)\) là điểm cần tìm.
Sách thầy cô Vietjack biên soạn
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Số các giá trị nguyên của m để hàm số \[f\left( x \right) = \frac{1}{3}{x^3} - \left( {m + 50} \right){x^2} + \left( {{m^2} + 100m} \right)x + 2020m\] nghịch biến trên \[\left( {7;13} \right)\] là
Xem đáp án »
28/06/2022
4,398
Câu 2:
Cho phương trình \[{\log _3}^2\left( {9x} \right) - \left( {m + 5} \right){\log _3}x + 3m - 10 = 0\]. Số giá trị nguyên của tham số m để phương trình đã cho có hai nghiệm phân biệt thuộc \[\left[ {1;81} \right]\] là
Xem đáp án »
28/06/2022
3,466
Câu 3:
Cho khối chóp S.ABCD có đáy là hình vuông cạnh \[2a\], cạnh bên \[SA\] vuông góc với mặt phẳng đáy, mặt bên \[(SBC)\] tạo với đáy một góc \[{30^0}\].Thể tích của khối chóp đã cho bằng
Xem đáp án »
28/06/2022
2,685
Câu 4:
Biết \[\int\limits_4^5 {\frac{{dx}}{{{x^2} + 3x + 2}} = a\ln 2 + b\ln 3 + c\ln 5 + d\ln 7} \] với \[a,b,c,d\] là các số nguyên. Tính \[P = ab + cd.\]
Xem đáp án »
28/06/2022
2,663
Câu 6:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \[{d_1}:\;\frac{{x - 2}}{{ - 1}} = \frac{{y - 1}}{3} = \frac{{z - 1}}{2}\] và \[{d_2}:\;\left\{ \begin{array}{l}x = 1 - 3t\\y = - 2 + t\\z = - 1 - t\end{array} \right..\] Phương trình đường thẳng \[\Delta \] nằm trong mặt phẳng \[\left( P \right):\;x + 2y - 3z - 2 = 0\] cắt cả hai đường thẳng \[{d_1}\] và \[{d_2}\] là
Xem đáp án »
28/06/2022
2,074
Câu 7:
Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng \[x = 1\] và \[x = 4\], biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục \[Ox\] tại điểm có hoành độ \[x\] (\[1 \le x \le 4\]) thì được thiết diện là một hình lục giác đều có độ dài cạnh là \[2x\].
Xem đáp án »
28/06/2022
1,595
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
45 bài tập Xác suất có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận