Câu hỏi:
13/04/2022 4,234Trong mặt phẳng cho 40 điểm tạo thành đa giác đều. Lấy ngẫu nhiên 4 điểm, tính xác suất sao cho 4 điểm này tạo thành hình chữ nhật mà không phải là hình vuông.
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn đáp án C
Lấy 4 điểm bất kì từ 40 điểm nên số phần tử của không gian mẫu là \(n\left( \Omega \right) = C_{40}^4\).
Ta có 40 điểm đã cho tạo thành đa giác đều nội tiếp trong đường tròn tâm O. Đánh số các điểm này theo thứ tự từ 1 đến 40, 40 điểm này tạo nên 20 đường kính của đường tròn (O). Mỗi hình chữ nhật được tạo nên bởi 2 đường chéo là 2 đường kính nên số hình chữ nhật (kể cả hình vuông) được tạo nên từ 4 đỉnh của đa giác đều là \(C_{20}^2\).
Ta tính số hình vuông: Mỗi hình vuông được tạo nên bởi 2 đường kính vuông góc. Với mỗi đường kính tồn tại duy nhất một đường kính vuông góc với nó. Vậy có 20 hình vuông, nhưng mỗi hình vuông bị lặp lại 2 lần nên có 20:2=10 (hình vuông).
Vậy số hình chữ nhật mà không là hình vuông là \(C_{20}^2 - 10\).
Xác suất cần tìm là \(P = \frac{{C_{20}^2 - 10}}{{C_{40}^4}} = \frac{{18}}{{9139}}\).
Chú ý: Có thể đếm số hình vuông theo cách 2 như sau: Chọn đáp ánđỉnh đầu tiên của hình vuông - có 40 cách Chọn đáp án; với mỗi cách Chọn đáp ánmột đỉnh thì luôn có một cách Chọn đáp ánduy nhất 3 đỉnh còn lại để tạo thành hình vuông (2 đỉnh liên tiếp của hình vuông hơn kém nhau 10 đơn vị, ví dụ ta Chọn đáp ánđỉnh đầu tiên là đỉnh số 1 thì 3 đỉnh còn lại là các đỉnh số 11, 21,31). Như vậy Chọn đáp ánđược 40 hình vuông, tuy nhiên mỗi hình vuông đã được tính lặp 4 lần nên số hình vuông thực tế là \(40:4 = 10\)(hình vuông).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn đáp án A
Hàm số \(y = {\log _3}\left( {x - 1} \right)\) có nghĩa khi \(x - 1 >0 \Rightarrow x >1\).
Vậy tập xác định của hàm số \(y = {\log _3}\left( {x - 1} \right)\) là \(\left( {1; + \infty } \right)\).
Lời giải
Chọn đáp án D
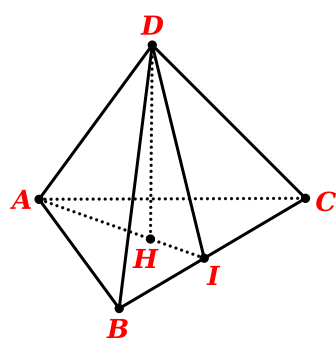
Gọi tứ diện \[ABCD\] là tứ diện đều cạnh a.
Gọi \[H\] là tâm của tam giác\[ABC\]. Khi đó \(DH \bot \left( {ABC} \right)\) tại \[H\].
Gọi \(I\) là trung điểm của \[BC\]. Khi đó góc giữa mặt phẳng \(\left( {DBC} \right)\) và \(\left( {ABC} \right)\) là góc \(\widehat {DIH}\)
Ta có \(\cos \widehat {\left( {\left( {ABC} \right),\left( {DBC} \right)} \right)} = \cos \widehat {DIH} = \frac{{IH}}{{ID}}\).
Tam giác \[ABC\] đều \( \Rightarrow IH = \frac{1}{3}IA = \frac{1}{3}.\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{6}\).
Tam giác \[DBC\] đều \( \Rightarrow ID = \frac{{a\sqrt 3 }}{2} \Rightarrow \cos \widehat {\left( {\left( {ABC} \right),DBC} \right)} = \frac{1}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải