Câu hỏi:
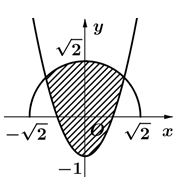
15/04/2022 2,160Cho (H) là hình phẳng giới hạn bởi parabol \[y = 2{x^2} - 1\] và nửa đường tròn có phương trình \[y = \sqrt {2 - {x^2}} \] (với \[ - \sqrt 2 \le x \le \sqrt 2 \]) (phần gạch chéo trong hình vẽ). Diện tích của (H) bằng
Câu hỏi trong đề: Bộ đề minh họa môn Toán THPT Quốc gia năm 2022 (30 đề) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn đáp án C
Phương trình hoành độ giao điểm của hai đồ thị là: \[2{x^2} - 1 = \sqrt {2 - {x^2}} \]
\[ \Leftrightarrow \left\{ \begin{array}{l}2{x^2} - 1 \ge 0\\4{x^4} - 4{x^2} + 1 = 2 - {x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2{x^2} - 1 \ge 0\\4{x^4} - 3{x^2} - 1 = 0\end{array} \right. \Leftrightarrow {x^2} = 1 \Leftrightarrow x = \pm 1\].
Diện tích hình \[\left( H \right)\] bằng: \[S = 2\int\limits_0^1 {\left( {\sqrt {2 - {x^2}} - 2{x^2} + 1} \right)dx} = 2\int\limits_0^1 {\sqrt {2 - {x^2}} dx} + 2\int\limits_0^1 {\left( { - 2{x^2} + 1} \right)dx} \]
\[ = 2{I_1} + \left. {2\left( {\frac{{ - 2{x^3}}}{3} + x} \right)} \right|_0^1 = 2{I_1} + \frac{2}{3}\].
Tính \[{I_1} = \int\limits_0^1 {\sqrt {2 - {x^2}} dx} \] đặt \[x = \sqrt 2 \sin t \Rightarrow dx = \sqrt 2 \cos tdt\] với \[t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\]
Đổi cận\[\left| \begin{array}{l}x = 0 \Rightarrow t = 0\\x = 1 \Rightarrow t = \frac{\pi }{4}\end{array} \right.\]\[ \Rightarrow {I_1} = \int\limits_0^{\frac{\pi }{4}} {\sqrt {2 - 2{{\sin }^2}t} .\sqrt 2 \cos tdt} = \int\limits_0^{\frac{\pi }{4}} {2{{\cos }^2}tdt} = \int\limits_0^{\frac{\pi }{4}} {\left( {1 + \cos 2t} \right)dt} \]
\[ = \left. {\left( {t + \frac{{\sin 2t}}{2}} \right)} \right|_0^{\frac{\pi }{4}} = \frac{\pi }{4} + \frac{1}{2} \Rightarrow S = 2{I_1} + \frac{2}{3} = \frac{\pi }{2} + 1 + \frac{2}{3} = \frac{{3\pi + 10}}{6}\].
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn đáp án B
Hàm số đã cho đã xác định và liên tục trên \(\left[ {1;4} \right]\).
Ta có \(\left\{ \begin{array}{l}x \in \left( {1;4} \right)\\y' = 2x - \frac{{16}}{{{x^2}}} = 0\end{array} \right. \Leftrightarrow x = 2\).
Tính \(y\left( 1 \right) = 17;{\rm{ }}y\left( 4 \right) = 20;{\rm{ }}y\left( 2 \right) = 12 \Rightarrow \mathop {\min }\limits_{\left[ {1;4} \right]} y = 12\)
Lời giải
Chọn đáp án D
Kẻ \(AK \bot d{\rm{ }}\left( {K \in d} \right) \Rightarrow K\left( {t + 1;1 - t;t + 1} \right) \Rightarrow \overrightarrow {AK} = \left( {t - 1;2 - t;t + 3} \right)\).
Ép cho \(AK \bot d \Leftrightarrow \overrightarrow {AK} .\overrightarrow {{u_d}} = 0 \Leftrightarrow \left( {t - 1} \right) + \left( {t - 2} \right) + \left( {t + 3} \right) = 0 \Leftrightarrow t = 0\)
\( \Rightarrow K\left( {1;1;1} \right) \Rightarrow \overrightarrow {KA} = \left( {1; - 2; - 3} \right) \Rightarrow KA = \sqrt {14} \).
Kẻ \(KH \bot \left( P \right) \Rightarrow d\left( {d;\left( P \right)} \right) = d\left( {K;\left( P \right)} \right) = KH \le KA = \sqrt {14} \)
Dấu “=” xảy ra khi \(\left( P \right)\) qua Avà vuông góc với KA.
Khi đó \(\left( P \right)\) nhận \(\overrightarrow {KA} = \left( {1; - 2; - 3} \right)\) là một VTPT.
Vậy \(\left( P \right)\) vuông góc với mặt phẳng có phương trình \(3x + z + 2 = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
30 Đề thi thử thpt quốc gia môn Toán có lời giải chi tiết mới nhất (Đề số 1)
-
CÂU TRẮC NGHIỆM ĐÚNG SAI
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 1)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 2)
-
Đề minh họa tốt nghiệp THPT môn Toán có đáp án năm 2025 (Đề 19)
-
(2025 mới) Đề thi ôn tập THPT môn Toán có đáp án (Đề số 2)
-
45 bài tập Xác suất có lời giải