Câu hỏi:

19/04/2022 2,036

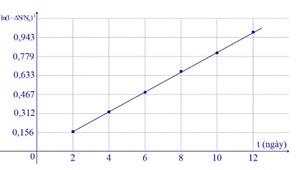
Trong phòng thí nghiệm, người ta tiến hành xác định chu kì bán rã T của một chất phóng xạ bằng cách dùng máy đếm xung để đo tỉ lệ giữa số hạt bị phân rã ΔN và số hạt ban đầu N₀. Dựa vào kết quả thực nghiệm đo được trên đồ thị hãy tính chu kì bán rã của chất phóng xạ này?

A. 5,6 ngày

B. 8,9 ngày

C. 3,8 ngày

D. 138 ngày

Xem lời giải

Câu hỏi trong đề: ĐGTD ĐH Bách khoa - Vấn đề thuộc lĩnh vực vật lí - Phóng xạ !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Trả lời:

Ta có: \[N = {N_0}{e^{ - \lambda t}}\]

→ Số hạt bị phân rã là:

\[\Delta N = {N_0} - {N_0}{e^{ - \lambda t}} = {N_0}\left( {1 - {e^{ - \lambda t}}} \right)\]

\[ \Rightarrow \frac{{\Delta N}}{{{N_0}}} = 1 - {e^{ - \lambda t}}\]

\[ \Rightarrow 1 - \frac{{\Delta N}}{{{N_0}}} = {e^{ - \lambda t}}\]

\[ \Rightarrow \frac{1}{{\left( {1 - \frac{{\Delta N}}{{{N_0}}}} \right)}} = {e^{\lambda t}}\]

\[ \Rightarrow \ln {\left( {1 - \frac{{\Delta N}}{{{N_0}}}} \right)^{ - 1}} = \lambda t\]

Từ đồ thị ta thấy: \[\lambda \approx 0,078\]

\[ \Rightarrow T = \frac{{\ln 2}}{\lambda } \approx 8,9\](ngày)

Đáp án cần chọn là: B

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một chất phóng xạ có chu kỳ bán rã là 3,8 ngày. Sau thời gian 11,4 ngày thì độ phóng xạ (hoạt độ phóng xạ) của lượng chất phóng xạ còn lại bằng bao nhiêu phần trăm so với độ phóng xạ của lượng chất phóng xạ ban đầu?

A. 25%

B. 75%

C. 12,5%

D. 87,5%

Lời giải

Trả lời:

T = 3,8 ngày ; t = 11,4 = 3T ngày. Do đó ta đưa về hàm mũ để giải nhanh như sau:

\[H = {H_0}{.2^{ - \frac{t}{T}}}\]

\[ \Leftrightarrow \frac{H}{{{H_0}}} = {2^{ - \frac{t}{T}}}\]

\[ \Leftrightarrow \frac{H}{{{H_0}}} = {2^{ - 3}} = \frac{1}{8} = 12,5\% \]

Đáp án cần chọn là: C

Câu 2

Hạt nhân \[{}_{92}^{234}U\] đang đứng yên thì phân rã phóng xạ ra hạt α. Thực nghiệm đo được động năng của hạt α bằng 12,89 MeV. Sự sai lệch giữa giá trị tính toán và giá trị đo được đã giải thích bằng việc phát ra bức xạ γ cùng hay với hạt αα trong quá trình phân rã \[{}_{92}^{234}U\]. Khối lượng hạt nhân \[{}_{92}^{234}U,{}_{90}^{230}Th\] và hạt α lần lượt bằng 233,9904u: 229,9737u và 4,0015lu. Biết rằng hằng số Planck, vận tốc ánh sáng trong chân không và điện tích nguyên tố có giá trị lần lượt bằng 6,625.10^-34J.s; 3.10⁸m/svà 1,6.10^-19C. Cho biết lu = 931,5 MeV/c². Bước sóng của bức xạ γ phát ra là:

A. 1,22.10^-9m

B. 1,22.10^-6m

C. 1,22.10^-12m

D. 1,22.10^-8m

Lời giải

Trả lời:

Ta có:

$\frac{h c}{λ} = W_{α} - W_{α}^{'}$

$\Leftrightarrow \frac{h c}{λ} = \frac{m_{T h}}{m_{T h} + m_{α}} (m_{U} - m_{T h} - m_{α}) - W_{α}^{'}$

\[ \Leftrightarrow \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{\lambda } = \frac{{229,9737u}}{{229,9737u + 4,00151u}}\]

\[.\left( {233,9904u - 229,9737u - 4,00151u} \right).{c^2} - 12,89MeV\]

\[ \Leftrightarrow \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{\lambda } = 0,983.0,01519u.{c^2} - 12,89MeV\]

\[ \Leftrightarrow \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{\lambda } = 0,983.0,01519.\frac{{931,5MeV}}{{{c^2}}}.{c^2} - 12,89MeV\]

\[ \Leftrightarrow \lambda = \frac{{6,{{625.10}^{ - 34}}{{.3.10}^8}}}{{\left( {0,983.0,01519.931,5 - 12,89} \right){{.10}^6}.1,{{6.10}^{ - 19}}}}\]

\[ \Leftrightarrow \lambda = 1,{22.10^{ - 12}}\left( m \right)\]

Đáp án cần chọn là: C

Câu 3

Đồng vị \[{}_{11}^{24}Na\]là chất phóng xạ β^- tạo thành hạt nhân magiê( \[{}_{12}^{24}Mg\]). Ban đầu có 12gam Na và chu kì bán rã là 15 giờ. Sau 45 h thì khối lượng Mg tạo thành là :

A. 10,5 g

B. 5,16 g

C.51,6 g

D. 0,516 g

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Chất Iốt phóng xạ \[{}_{53}^{131}I\] dùng trong y tế có chu kỳ bán rã 8 ngày đêm. Nếu nhận được 100g chất này thì sau 8 tuần lễ còn bao nhiêu?

A. 0,87g

B. 0,78g

C. 7,8g

D. 8,7g

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Pôlôni \[{}^{210}Po\] là một chất phóng xạ có chu kì bán rã 140 ngày đêm. Hạt nhân pôlôni phóng xạ sẽ biến thành hạt nhân chì (\[{}^{210}Po\]) và kèm theo một hạt a. Ban đầu có 42mg chất phóng xạ pôlôni. Khối lượng chì sinh ra sau 280 ngày đêm là:

A. 30,9 mg

B. 10,35 mg

C. 31,96 mg

D. 10,65 mg

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Gọi N₀ là số hạt nhân phóng xạ ban đầu (t = 0) và ΔN là số hạt nhân đã phóng xạ sau thời gian t. Đồ thị nào sau đây biểu thị sự biến thiên của ΔN theo thời gian?

A. Hình A

B. Hình B

C. Hình C

D. Hình D

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Một chất phóng xạ có chu kỳ bán rã là 3,8 ngày. Sau thời gian 11,4 ngày thì độ phóng xạ (hoạt độ phóng xạ) của lượng chất phóng xạ còn lại bằng bao nhiêu phần trăm so với độ phóng xạ của lượng chất phóng xạ ban đầu?

Đồng vị \[{}_{11}^{24}Na\]là chất phóng xạ β- tạo thành hạt nhân magiê( \[{}_{12}^{24}Mg\]). Ban đầu có 12gam Na và chu kì bán rã là 15 giờ. Sau 45 h thì khối lượng Mg tạo thành là :

Chất Iốt phóng xạ \[{}_{53}^{131}I\] dùng trong y tế có chu kỳ bán rã 8 ngày đêm. Nếu nhận được 100g chất này thì sau 8 tuần lễ còn bao nhiêu?

Gọi N0 là số hạt nhân phóng xạ ban đầu (t = 0) và ΔN là số hạt nhân đã phóng xạ sau thời gian t. Đồ thị nào sau đây biểu thị sự biến thiên của ΔN theo thời gian?

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Đồng vị \[{}_{11}^{24}Na\]là chất phóng xạ β^- tạo thành hạt nhân magiê( \[{}_{12}^{24}Mg\]). Ban đầu có 12gam Na và chu kì bán rã là 15 giờ. Sau 45 h thì khối lượng Mg tạo thành là :

Gọi N₀ là số hạt nhân phóng xạ ban đầu (t = 0) và ΔN là số hạt nhân đã phóng xạ sau thời gian t. Đồ thị nào sau đây biểu thị sự biến thiên của ΔN theo thời gian?