“Sự lão hóa bình thường” được nhắc đến ở đoạn số 2 nghĩa là gì?
“Sự lão hóa bình thường” được nhắc đến ở đoạn số 2 nghĩa là gì?
A. Những vấn đề mà bác sĩ chấp nhận là bình thường ở người già trong giai đoạn trước.
B. Sự lão hóa theo quy luật tự nhiên.
C. Sự lão hóa không bị gây ra bởi tác nhân bên ngoài.
Quảng cáo
Trả lời:
Chọn A
Phương pháp giải:
Dựa vào nội dung đoạn trích, phân tích.
Giải chi tiết:
Sự lão hóa bình thường được hiểu là: Những vấn đề mà bác sĩ chấp nhận là bình thường ở người già trong giai đoạn trước.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chọn D
Phương pháp giải:
Gọi điểm C thỏa mãn MA = 2MC
GTNN của MA + 2MB là BC
Tìm giao của BC với mặt cầu, chính là điểm M cần tìm
Giải chi tiết:
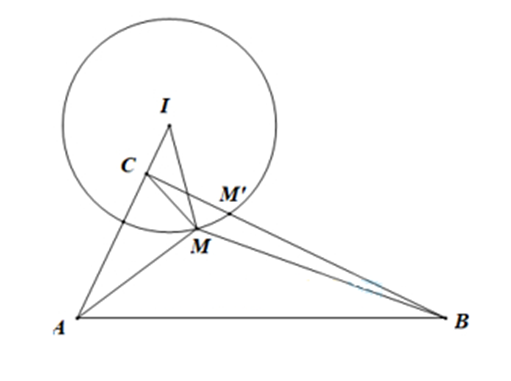
Mặt cầu (S) có tâm và bán kính . Có
Gọi C là điểm thỏa mãn
Có . IA (c. g.c)
Đẳng thức xảy ra khi M trùng M ' là giao của đoạn BC với (S)
M’ thuộc đoạn BC
. Ta có
Vậy .
Câu 2
Lời giải
Chọn C
Phương pháp giải:
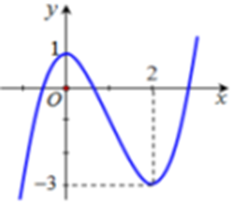
Cách tìm số các tiệm cận:
+ Tiệm cận ngang: Cho x tiến tới dương vô cùng và âm vô cùng
+ Tiệm cận đứng: Tìm các nghiệm của mẫu thức, loại đi các nghiệm không phù hợp.
Giải chi tiết:
ĐK: {x≤2f2(x)+3f(x)≠0{x≤2f2(x)+3f(x)≠0
+ Tiệm cận ngang:
Vì hàm số y là hàm số phân thức, có bậc của tử nhỏ hơn bậc của mẫu nên .
⇒ Đồ thị có 1 TCN y=0.
+ Tiệm cận đứng:
Ta có
Vì x=2 là nghiệm kép của mẫu, nên mẫu sẽ có nhân tử . Do đó x=2 là một TCĐ.
Suy ra đồ thị hàm số có 4 TCĐ.
Vậy tổng số tiệm cận là 5.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.