Câu hỏi:

05/05/2022 2,147

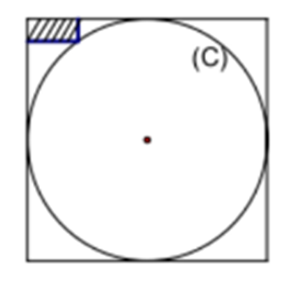
Một thợ mộc chế tạo một đồ vật hình trụ từ một khối gỗ hình hộp chữ nhật, có đáy là hình vuông và chiều cao bằng 1,25m bằng cách vẽ hai đường tròn (C) và (C’) nội tiếp hai đáy để tạo ra hai đáy của hình trụ, rồi bỏ đi phần gỗ thừa bên ngoài khối trụ. Biết rằng trong tam giác cong tạo bởi (C) và hình vuông đáy có một hình chữ nhật kích thước 0,3cm x 0,6cm (như hình). Hỏi 10 đồ vật như vậy người thợ mộc sẽ bán được số tiền gần nhất với giá trị nào sau đây, biết giá tiền trung bình của đồ vật tính theo mỗi mét khối là 20 triệu đồng?

A. 196 nghìn đồng

B. 65 nghìn đồng

C. 176 nghìn đồng

D. 58 nghìn đồng

Xem lời giải

Câu hỏi trong đề: Đề thi Đánh giá tư duy Đọc hiểu, Toán học - ĐH Bách khoa năm 2023 - 2024 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn C

Phương pháp giải:

Tính bán kính đáy của đồ vật

Tính thể tích của 1 đồ vật và 10 đồ vật.

Tính giá tiền

Giải chi tiết:

Gọi bán kính đáy của đồ vật là x (cm) (x > 0,6).

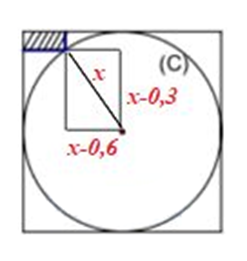
Một thợ mộc chế tạo một đồ vật hình trụ từ một khối gỗ hình hộp chữ nhật, có đáy là hình vuông và chiều cao bằng 1,25m (ảnh 2)

Ta có phương trình

${(x - 0, 3)}^{2} + {(x - 0, 6)}^{2} = x^{2} \Leftrightarrow x^{2} - 1, 8 x + 0, 45 = 0 \Leftrightarrow [\begin{array}{l} x = \frac{3}{2} (t m) \\ x = \frac{3}{10} (k t m) \end{array}$

Thể tích của 1 và 10 đồ vật lần lượt là

$\begin{array}{l} V_{1} = π .0, 015^{2} .1, 25 \\ V_{10} = 10 π .0, 015^{2} .1, 25 \end{array}$

Số tiền thu được là $T_{10} = 20000.10 π .0, 015^{2} .1, 25 \approx 176, 7$ (nghìn đồng)

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong không gian Oxyz cho mặt cầu $(S) : {(x - 1)}^{2} + y^{2} + {(z - 2)}^{2} = 10$ và hai điểm A(1;2;-4); B(1;2;14). Điểm M(a;b;c) là điểm nằm trên mặt cầu (S) sao cho P = MA + 2MB đạt GTNN. Khi đó a+b+c bằng:

A. $\frac{7}{41}$

B. $\frac{23}{41}$

C. 4

D. 7

Lời giải

Chọn D

Phương pháp giải:

Gọi điểm C thỏa mãn MA = 2MC

GTNN của MA + 2MB là BC

Tìm giao của BC với mặt cầu, chính là điểm M cần tìm

Giải chi tiết:

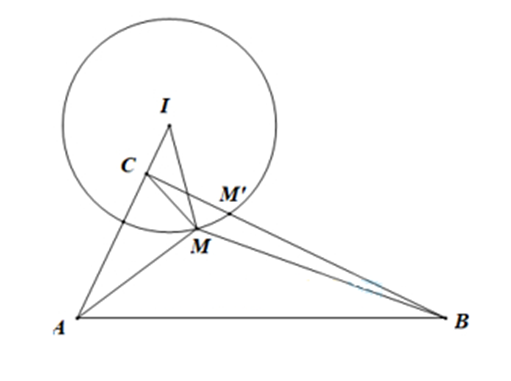
Trong không gian Õyz cho mặt cầu (S): (x-1)^2+y^2+(z-2)^2=10 và hai điểm A(1;2;-4) ;B(1;2;14) . Điểm M(a.b.c) là điểm nằm trên (ảnh 1)

Mặt cầu (S) có tâm $I (1; 0; 2)$ và bán kính $R = \sqrt{10}$ . Có

$\vec{IA} = (0; 2; - 6); IA = \sqrt{2^{2} + 6^{2}} = 2 \sqrt{10} = 2 R$

Gọi C là điểm thỏa mãn $\vec{I C} = \frac{1}{4} \vec{I A} = (0; \frac{1}{2}; - \frac{3}{2}) \Rightarrow C (1; \frac{1}{2}; \frac{1}{2})$

Có ${IM}^{2} = IC$ . IA $\Rightarrow Δ IMC ~ Δ IAM$ (c. g.c)

\Rightarrow \frac{MA}{MC} = \frac{IA}{IM} = 2 \Rightarrow MA = 2 MC \Rightarrow MA + 2 MB = 2 (MB + MC) \geq BC

Đẳng thức xảy ra khi M trùng M ' là giao của đoạn BC với (S)

M’ thuộc đoạn BC $\Leftrightarrow \vec{C M'} = k \vec{C B} = (0; \frac{3}{2} k; \frac{27}{2} k) (k > 0)$

$\Leftrightarrow M^{'} (1; \frac{1}{2} + \frac{3}{2} k; \frac{1}{2} + \frac{27}{2} k)$ . Ta có

M^{'} \in (S) \Leftrightarrow {IM}^{'} = \sqrt{10} \Leftrightarrow 0 + {(\frac{1}{2} + \frac{3}{2} k)}^{2} + {(\frac{27}{2} k - \frac{3}{2})}^{2} = 10

\Leftrightarrow k = \frac{1}{3} \Rightarrow M^{'} (1; 1; 5) .

Vậy $a + b + c = 7$ .

Câu 2

1. Tìm tất cả các giá trị của m để hàm số $y = \frac{1}{3} m x^{3} - (m - 1) x^{2} + 3 (m - 2) x + 2022$ đồng biến trên $[2; + \infty)$

2. Cho dãy số (u_n) có số hạng tổng quát $u_{1} = 1 - \frac{1}{{(n + 1)}^{2}}, \forall n \in ℕ *$ . Tính $l i m (u_{1} u_{2} ... u_{n})$

Xem đáp án

Lời giải

a) Phương pháp giải:

Hàm số đồng biến khi đạo hàm không âm.

Giải bất phương trình y’ ≥ 0 rồi cô lập m, lập bảng biến thiên trên khoảng cần xét.

Giải chi tiết:

Hàm số đã cho đồng biến trên nửa khoảng đã cho khi và chỉ khi

$y' = m x^{2} - 2 (m - 1) x + 3 (m - 2) \geq 0 \forall x \in [2; + \infty)$

$\Leftrightarrow m (x^{2} - 2 x + 3) \geq 6 - 2 x$

$\Leftrightarrow m \geq \frac{6 - 2 x}{x^{2} - 2 x + 3} (d o x^{2} - 2 x + 3 = {(x - 1)}^{2} + 2 > 0, \forall x)$

Xét $f (x) = \frac{6 - 2 x}{x^{2} - 2 x + 3}$ trên [2;+∞) có $f' (x) = \frac{2 x^{2} - 12 x + 6}{{(x^{2} - 2 x + 3)}^{2}} = 0 \Leftrightarrow x = 3 \pm \sqrt{6}$ .

Ta có BBT

1. Tìm tất cả các giá trị của m để hàm số y=1/3mx^3-(m-1)*x^2+3(m-2)*x+2022 đồng biến trên [2, dương vô cùng). (ảnh 1)

Căn cứ BBT, ta có các giá trị m cần tìm là $m \geq \frac{2}{3}$

Vậy $m \geq \frac{2}{3}$ .

b) Phương pháp giải:

Tìm số hạng tổng quát của dãy $u_{1} u_{2} ... u_{n}$ .

Từ đó tìm ra $l i m (u_{1} u_{2} ... u_{n})$ .

Giải chi tiết:

Ta có

$u_{n} = \frac{n^{2} + 2 n}{{(n + 1)}^{2}} = \frac{n (n + 2)}{{(n + 1)}^{2}}$

$\Rightarrow u_{1} = \frac{1.3}{2^{2}}; u_{2} = \frac{2.4}{3^{2}}; ...; u_{n} = \frac{n (n + 2)}{{(n + 1)}^{2}}$

$\Rightarrow u_{1} u_{2} ... u_{n} = \frac{1.2.3.4... n (n + 2)}{2^{2} {.3}^{2} ... {(n + 1)}^{2}} = \frac{n + 2}{2 (n + 1)}$

$\Rightarrow \lim (u_{1} u_{2} ... u_{n}) = \lim \frac{1 + \frac{2}{n}}{2 + \frac{2}{n}} = \frac{1}{2}$

Câu 3

Cho hàm số bậc ba $y = f (x)$ có đồ thị như hình vẽ. Tổng số đường tiệm cận của đồ thị hàm số $y = \frac{(x^{2} - 2 x) \sqrt{2 - x}}{(x - 3) [f^{2} (x) + 3 f (x)]}$ là?

A. 3

B. 4

C. 5

D. 6

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Trong ao có 10 lá sen thẳng hàng, nằm sát mặt nước. Một con ếch đứng ở chiếc lá sen đầu tiên và nó định nhảy đến chiếc lá cuối cùng. Mỗi lần nó có thể nhảy tiến tới tích 1 hoặc 2 bước (tức là không quay lại). Hòi nó có bao nhiêu cách nhảy để đến đích?

A. 47

B. 51

C. 54

D. 55

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Có 6 học sinh gồm 1 học sinh lớp 10, 2 học sinh lớp 11 và 3 học sinh lớp 12 được xếp ngẫu nhiên thành một hàng dọc. Xác suất học sinh lớp 10 đứng xen kẽ giữa 2 học sinh lớp 12 là:

A. $\frac{1}{10}$

B. $\frac{3}{5}$

C. $\frac{1}{5}$

D. $\frac{3}{10}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Tứ điện đều ABCD có cạnh a. Mặt cầu (S) tiếp xúc với AB, AC, AD lần lượt tại B, C, D giới hạn nên một hình cầu có thể tích là:

A. $\frac{π a^{3} \sqrt{3}}{2}$

B. $\frac{4 π a^{3}}{81}$

C. $\frac{π a^{3} \sqrt{2}}{3}$

D. $\frac{8 π a^{3}}{27}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Sự phân rã của một đồng vị phóng xạ được biểu diễn theo công thức $m (t) = m_{0} {(\frac{1}{2})}^{\frac{t}{r}}$ trong đó $m_{0}$ là khối lượng ban đầu của đồng vị phóng xạ (tại thời điểm $t = 0$ ); là chu kỳ bán rã của đồng vị đó. Biết rằng chu kỳ bán rã của đồng vị cacbon 14 (¹⁴C) là khoảng 5730 năm, hỏi một mẫu đồ cổ có độ tuổi là bao nhiêu năm biết rằng trong mẫu đồ cổ này chứa đồng vị cacbon 14 và đồng vị này đã mất khoảng 25% khối lượng ban đầu của nó?

A. 2300 năm

B. 2378 năm

C. 2387 năm

D. 2400 năm

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Trong không gian Oxyz cho mặt cầu (S):(x−1)2+y2+(z−2)2=10 và hai điểm A(1;2;-4); B(1;2;14). Điểm M(a;b;c) là điểm nằm trên mặt cầu (S) sao cho P = MA + 2MB đạt GTNN. Khi đó a+b+c bằng:

1. Tìm tất cả các giá trị của m để hàm số y=13mx3−(m−1)x2+3(m−2)x+2022 đồng biến trên [2;+∞) 2. Cho dãy số (un) có số hạng tổng quát u1=1−1n+12,∀n∈ℕ*. Tính limu1u2...un

Cho hàm số bậc ba y=f(x) có đồ thị như hình vẽ. Tổng số đường tiệm cận của đồ thị hàm số y=x2−2x2−x(x−3)f2(x)+3f(x) là?

Có 6 học sinh gồm 1 học sinh lớp 10, 2 học sinh lớp 11 và 3 học sinh lớp 12 được xếp ngẫu nhiên thành một hàng dọc. Xác suất học sinh lớp 10 đứng xen kẽ giữa 2 học sinh lớp 12 là:

Tứ điện đều ABCD có cạnh a. Mặt cầu (S) tiếp xúc với AB, AC, AD lần lượt tại B, C, D giới hạn nên một hình cầu có thể tích là:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Trong không gian Oxyz cho mặt cầu $(S) : {(x - 1)}^{2} + y^{2} + {(z - 2)}^{2} = 10$ và hai điểm A(1;2;-4); B(1;2;14). Điểm M(a;b;c) là điểm nằm trên mặt cầu (S) sao cho P = MA + 2MB đạt GTNN. Khi đó a+b+c bằng:

Cho hàm số bậc ba $y = f (x)$ có đồ thị như hình vẽ. Tổng số đường tiệm cận của đồ thị hàm số $y = \frac{(x^{2} - 2 x) \sqrt{2 - x}}{(x - 3) [f^{2} (x) + 3 f (x)]}$ là?