Câu hỏi:
12/07/2024 724
Cho hình lăng trụ đều \(ABC.A'B'C'\) có cạnh đáy bằng 2a, cạnh bên bằng a. Tính góc giữa hai mặt phẳng \(\left( {AB'C'} \right)\) và \(\left( {A'B'C'} \right)\)?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: \({30^0}\)
Phương pháp giải:
- Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Giải chi tiết:
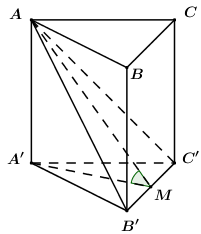
Gọi M là trung điểm của \(B'C'\), do tam giác \(A'B'C'\) đều nên \(A'M \bot B'C'\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{B'C' \bot A'M}\\{B'C' \bot AA'}\end{array}} \right. \Rightarrow B'C' \bot \left( {AA'M} \right)\), suy ra \(B'C' \bot AM\).
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{\left( {AB'C'} \right) \cap \left( {A'B'C'} \right) = B'C'}\\{AM \subset \left( {AB'C'} \right);{\mkern 1mu} {\mkern 1mu} AM \bot B'C'}\\{A'M \subset \left( {A'B'C'} \right);{\mkern 1mu} {\mkern 1mu} A'M \bot B'C'}\end{array}} \right.\)
\( \Rightarrow \angle \left( {\left( {AB'C'} \right);\left( {A'B'C'} \right)} \right) = \angle \left( {AM;A'M} \right) = \angle A'MA\).
Tam giác \(A'B'C'\) đều cạnh 2a nên \(A'M = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 \).
Xét tam giác vuông \[AA'M\] có: \(\tan \angle A'MA = \frac{{AA'}}{{A'M}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }}\)\[ \Rightarrow \angle A'MA = {30^0}\].
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp giải:
Căn cứ vào biện pháp tu từ.
Giải chi tiết:
- Biện pháp nghệ thuật sử dụng là ẩn dụ chuyển đổi cảm giác.
- Cho thấy niềm vui sướng và hạnh phúc của tác giả khi được chiến đấu dưới ngọn cờ của Đảng
- “Mặt trời chân lí” là hình ảnh ẩn dụ ca ngợi lí tưởng Cách mạng, ca ngợi chủ nghĩa Cộng sản đã soi sáng tâm hồn, đã “chói qua tim”, đem lại ánh sáng cuộc đời như “bừng” lên trong “nắng hạ”.
Lời giải
Phương pháp giải:
Căn cứ vào các thể loại.
Giải chi tiết:
Văn bản trên thuộc thể loại kí (bút kí).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử ĐGNL ĐHQG Hà Nội năm 2023-2024 (Đề 20)
-
Bộ 20 đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 15)
-
ĐGNL ĐHQG Hà Nội - Tư duy định tính - Tìm và phát hiện lỗi sai
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 30)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội năm 2024 - 2025 có đáp án (Đề 1)
-
Đề thi Đánh giá năng lực ĐHQG Hà Nội form 2025 có đáp án (Đề 3)