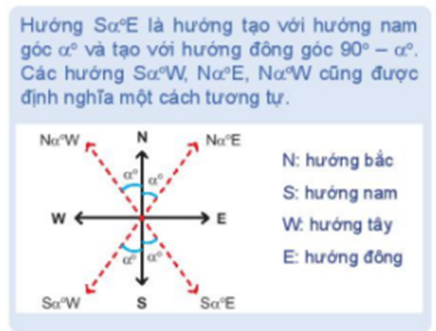
Từ một khu vực có thể quan sát hai đỉnh núi, ta có thể ngắm và đo để xác định khoảng cách giữa hai đỉnh núi đó. Hãy thảo luận để đưa ra các bước cho một cách đo.
Từ một khu vực có thể quan sát hai đỉnh núi, ta có thể ngắm và đo để xác định khoảng cách giữa hai đỉnh núi đó. Hãy thảo luận để đưa ra các bước cho một cách đo.
Câu hỏi trong đề: Bài tập Hệ thức lượng trong tam giác có đáp án !!
Quảng cáo
Trả lời:
Bước 1: Tại khu vực quan sát, đặt một cọc tiêu cố định tại vị trí A. Kí hiệu hai đỉnh núi lần lượt là điểm B và điểm C.
Đứng tại A, ngắm điểm B và điểm C để đo góc tạo bởi hai hướng ngắm đó.
Bước 2: Đo khoảng cách từ vị trí ngắm đến từng đỉnh núi, tức là tính AB, AC.
* Tính AB bằng cách:
+ Đứng tại A, ngắm đỉnh núi B để xác định góc ngắm so với mặt đất, kí hiệu là góc α.
+ Theo hướng ngắm, đặt tiếp cọc tiêu tại D gần đỉnh núi hơn và đo đoạn AD. Xác định góc ngắm tại điểm D, kí hiệu là góc β.
Ta có hình vẽ:
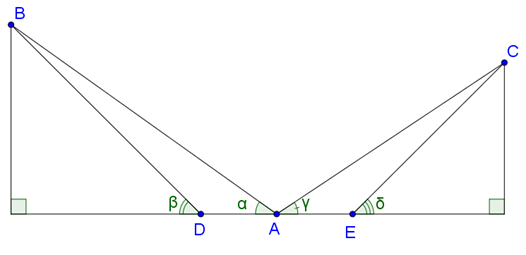
Ta có: ; .
Áp dụng định lí sin vào ∆ABD, ta được:
* Tương tự ngắm và đo để xác định AC.
Ta có: ; .
Áp dụng định lí sin vào ∆ACE, ta được:
Bước 3: Tính khoảng cách giữa hai đỉnh núi, bằng cách áp dụng định lí côsin cho tam giác ABC để tính độ dài cạnh BC.
Ta có: BC2 = AB2 + AC2 – 2AB.AC.cosBAC.
Với AB, AC, góc BAC đã biết ở các bước trên, thay vào ta tính được BC chính là khoảng cách giữa hai đỉnh núi.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
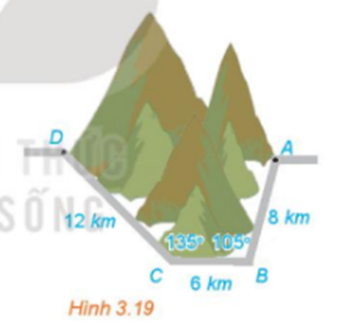
Ta có sơ đồ di chuyển của tàu như sau”
Trong đó: B là nơi động cơ bị hỏng, C là vị trí neo đậu của tàu trên hòn đảo.
Khoảng cách từ cảng A tới đảo nơi tàu neo đậu là đoạn AC (hay b).
Ban đầu tàu di chuyển theo hướng S70oE nên = 70o.
Sau khi động cơ bị hỏng, tàu trôi theo hướng Nam nên BC // AS.
.
Quãng đường tàu đi được sau 90 phút hay 1,5 giờ (ngay trước khi hỏng động cơ) là:
70 . 1,5 = 105 (km) hay c = 105.
Quãng đường tàu trôi tự do là:
8 . 2 = 16 (km) hay a = 16.
a) Áp dụng định lí cosin cho tam giác ABC, ta có:
b2 = a2 + c2 − 2ac . cosB
Þ b2 = 162 + 1052 – 2 . 16 . 105 . cos 110o ≈ 12 430,18
Þ b ≈ 111,49.
Vậy khoảng cách từ cảng A tới đảo nơi tàu neo đậu là khoảng 111,49 km.
b) Theo sơ đồ, hướng từ cảng A tới đảo nơi tàu neo đậu là SαoE với α = .
Áp dụng định lí sin cho tam giác ABC, ta có:
Mà ; b ≈ 111,49; a = 16.
Þ α ≈ 70° – 8° = 62°.
Vậy hướng từ cảng A đến đảo nơi tàu neo đậu là S62°E.
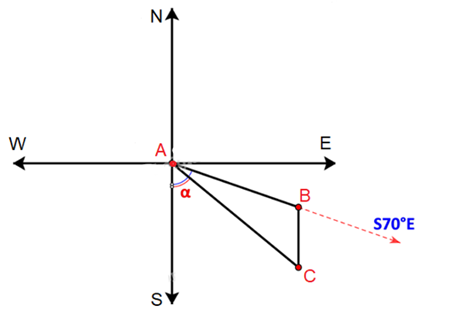
Lời giải
Ta có hình vẽ sau:
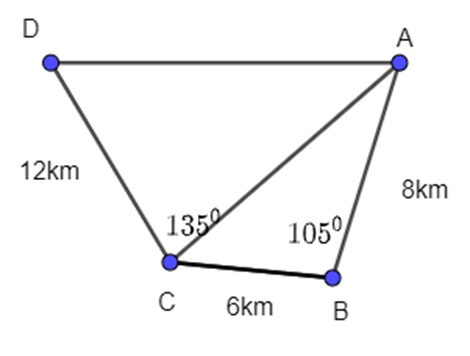
Bước 1: Áp dụng định lí côsin trong ΔABC, ta có:
AC2 = AB2 + BC2 – 2AB.BC.cosB (định lí cos)
= 82 + 62 – 2.8.6.cos1050≈ 124,85
⇒ AC ≈ 11,2 km.
Bước 2: Áp dụng định lí sin trong ΔABC, ta có:
Bước 3:
Áp dụng định lí côsin trong ΔACD, ta có:
AD2 = AC2 + DC2 – 2AC.DC.cosACD (định lí cos)
= 11,172 + 122 – 2.11,2.12.cos91,40
⇒ AD ≈ 16,6 km.
Bước 4: Độ dài đường mới giảm so với đường cũ là:
12 + 6 + 8 − 16,6 = 9,4 (km).
Vậy độ dài đường mới sẽ giảm 9,4 kilômét so với đường cũ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.