Ta đã biết tính cosA theo độ dài các cạnh của tam giác ABC. Liệu sinA và diện tích S có tính được theo độ dài cạnh của tam giác ABC không?

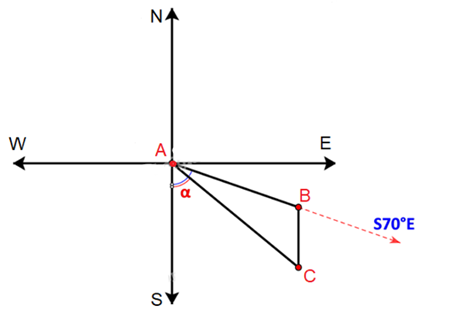
Trong đó: B là nơi động cơ bị hỏng, C là vị trí neo đậu của tàu trên hòn đảo.

Khoảng cách từ cảng A tới đảo nơi tàu neo đậu là đoạn AC (hay b).

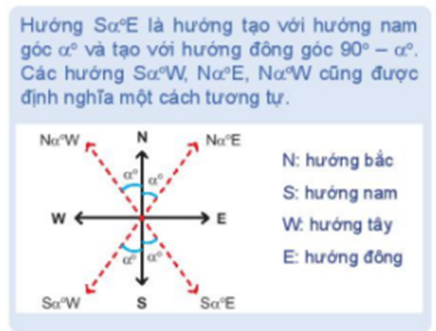
Ban đầu tàu di chuyển theo hướng S70^oE nên  = 70^o.

Sau khi động cơ bị hỏng, tàu trôi theo hướng Nam nên BC // AS.

$\Rightarrow \widehat{ABC}={180}^o-\widehat{BAS}={110}^o$.

Quãng đường tàu đi được sau 90 phút hay 1,5 giờ (ngay trước khi hỏng động cơ) là:

70 . 1,5 = 105 (km) hay c = 105.

Quãng đường tàu trôi tự do là:

8 . 2 = 16 (km) hay a = 16.

a) Áp dụng định lí cosin cho tam giác ABC, ta có:

b² = a² + c² − 2ac . cosB

Þ b² = 16² + 105² – 2 . 16 . 105 . cos 110^o ≈ 12 430,18

Þ b ≈ 111,49.

Vậy khoảng cách từ cảng A tới đảo nơi tàu neo đậu là khoảng 111,49 km.

b) Theo sơ đồ, hướng từ cảng A tới đảo nơi tàu neo đậu là Sα^oE với α = .

Áp dụng định lí sin cho tam giác ABC, ta có:

$$\begin{gathered} \frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C} \\ \Rightarrow \sin A=\frac{{\displaystyle a.\sin B}}{{\displaystyle b}} \end{gathered}$$

Mà$\widehat{B}={110}^o$ ; b ≈ 111,49; a = 16.

$$\begin{gathered} \Rightarrow \sin A=\frac{16.\sin 110°}{\mathrm{111,49}}\approx \mathrm{0,135} \\ \Rightarrow \widehat{A}\approx 8° (do \widehat{A}<90° ). \end{gathered}$$

Þ α ≈ 70° – 8° = 62°.

Vậy hướng từ cảng A đến đảo nơi tàu neo đậu là S62°E.

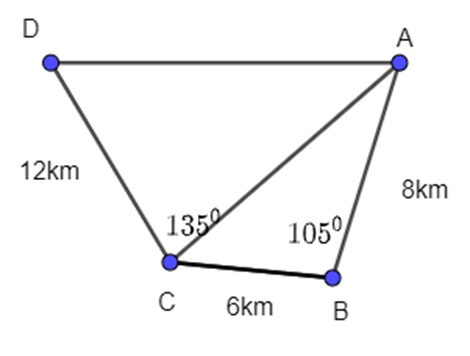
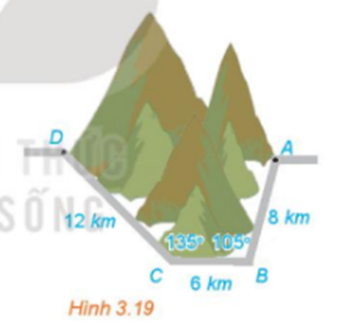
Bước 1: Áp dụng định lí côsin trong ΔABC, ta có:

Bước 2: Áp dụng định lí sin trong ΔABC, ta có:

Bước 3:

Áp dụng định lí côsin trong ΔACD, ta có:

Bước 4: Độ dài đường mới giảm so với đường cũ là: 

12 + 6 + 8 − 16,6 = 9,4 (km).

Vậy độ dài đường mới sẽ giảm 9,4 kilômét so với đường cũ.