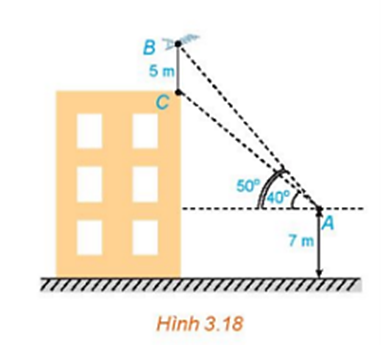
Trên nóc một tòa nhà có một cột ăng – ten cao 5m, Từ một vị trí quan sát A cao 7m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng – ten, với các góc tương ứng là 500 và 400 so với phương nằm ngang (H.3.18).
a) Tính các góc của tam giác ABC.
b) Tính chiều cao của tòa nhà.
Trên nóc một tòa nhà có một cột ăng – ten cao 5m, Từ một vị trí quan sát A cao 7m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng – ten, với các góc tương ứng là 500 và 400 so với phương nằm ngang (H.3.18).
a) Tính các góc của tam giác ABC.
b) Tính chiều cao của tòa nhà.

Câu hỏi trong đề: Bài tập Hệ thức lượng trong tam giác có đáp án !!
Quảng cáo
Trả lời:
Ta có hình vẽ sau:
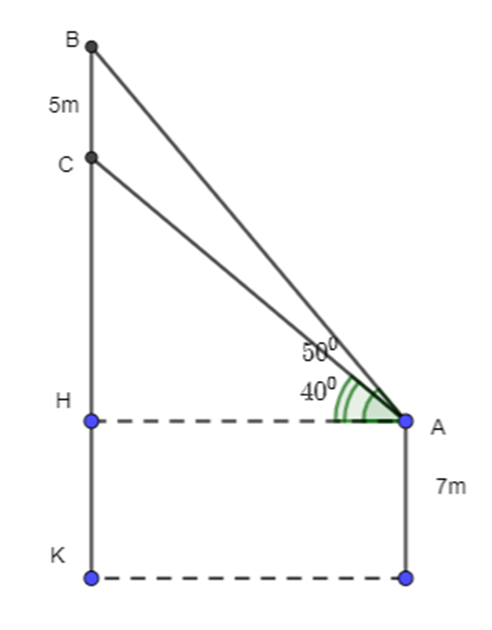
a) Ta có:
Xét ΔABH, vuông tại H, có: (hai góc phụ nhau)
Xét ΔABC, có:
b) Áp dụng định lí sin cho tam giác ABC, ta được:
.
Xét ΔABH, có:
Do đó chiều cao của tòa nhà là: 16,9 + 7 = 23,9 (m).
Vậy chiều cao của tòa nhà xấp xỉ bằng 23,9 m.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có sơ đồ di chuyển của tàu như sau”
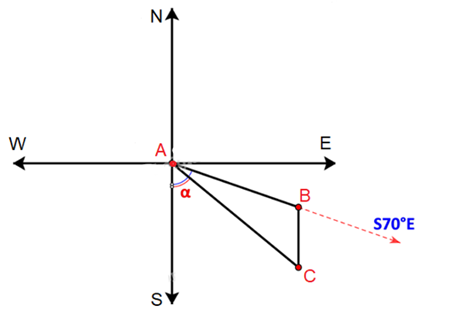
Trong đó: B là nơi động cơ bị hỏng, C là vị trí neo đậu của tàu trên hòn đảo.
Khoảng cách từ cảng A tới đảo nơi tàu neo đậu là đoạn AC (hay b).
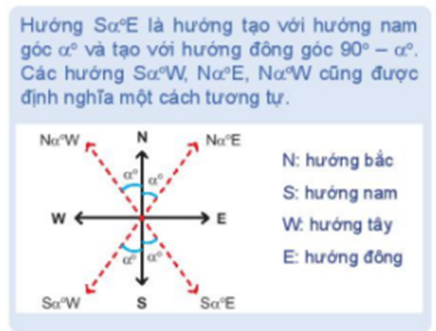
Ban đầu tàu di chuyển theo hướng S70oE nên = 70o.
Sau khi động cơ bị hỏng, tàu trôi theo hướng Nam nên BC // AS.
.
Quãng đường tàu đi được sau 90 phút hay 1,5 giờ (ngay trước khi hỏng động cơ) là:
70 . 1,5 = 105 (km) hay c = 105.
Quãng đường tàu trôi tự do là:
8 . 2 = 16 (km) hay a = 16.
a) Áp dụng định lí cosin cho tam giác ABC, ta có:
b2 = a2 + c2 − 2ac . cosB
Þ b2 = 162 + 1052 – 2 . 16 . 105 . cos 110o ≈ 12 430,18
Þ b ≈ 111,49.
Vậy khoảng cách từ cảng A tới đảo nơi tàu neo đậu là khoảng 111,49 km.
b) Theo sơ đồ, hướng từ cảng A tới đảo nơi tàu neo đậu là SαoE với α = .
Áp dụng định lí sin cho tam giác ABC, ta có:
Mà ; b ≈ 111,49; a = 16.
Þ α ≈ 70° – 8° = 62°.
Vậy hướng từ cảng A đến đảo nơi tàu neo đậu là S62°E.
Lời giải
Ta có hình vẽ sau:
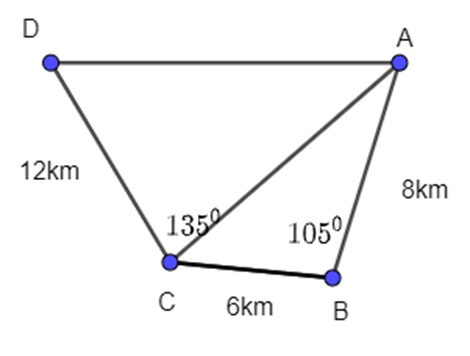
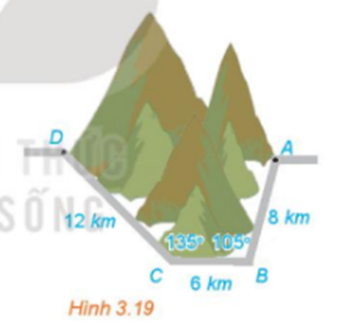
Bước 1: Áp dụng định lí côsin trong ΔABC, ta có:
AC2 = AB2 + BC2 – 2AB.BC.cosB (định lí cos)
= 82 + 62 – 2.8.6.cos1050≈ 124,85
⇒ AC ≈ 11,2 km.
Bước 2: Áp dụng định lí sin trong ΔABC, ta có:
Bước 3:
Áp dụng định lí côsin trong ΔACD, ta có:
AD2 = AC2 + DC2 – 2AC.DC.cosACD (định lí cos)
= 11,172 + 122 – 2.11,2.12.cos91,40
⇒ AD ≈ 16,6 km.
Bước 4: Độ dài đường mới giảm so với đường cũ là:
12 + 6 + 8 − 16,6 = 9,4 (km).
Vậy độ dài đường mới sẽ giảm 9,4 kilômét so với đường cũ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.