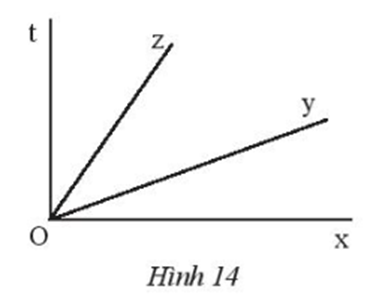
a) Quan sát Hình 1 và cho biết hai góc và có:
- Cạnh nào chung?
- Điểm trong nào chung?
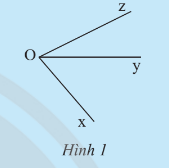
b) Hãy đo các góc trong Hình 1 rồi so sánh tổng số đo của và với .
c) Tính tổng số đo của hai góc và trong Hình 2.
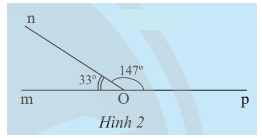
a) Quan sát Hình 1 và cho biết hai góc và có:
- Cạnh nào chung?
- Điểm trong nào chung?

b) Hãy đo các góc trong Hình 1 rồi so sánh tổng số đo của và với .
c) Tính tổng số đo của hai góc và trong Hình 2.

Câu hỏi trong đề: Bài tập Các góc ở vị trí đặc biệt có đáp án !!
Quảng cáo
Trả lời:
a) Trong Hình 1:
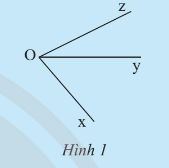
Hai góc và có cạnh Oy chung và không có điểm trong chung.
b) Đo các góc trong Hình 1, ta được:
.
Ta có: .
Do đó, .
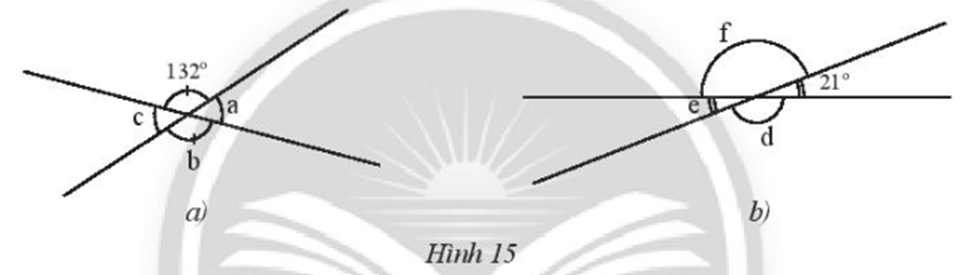
c) Trong Hình 2:
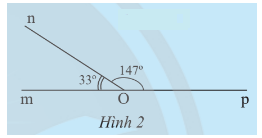
Ta có: .
Vậy tổng số đo của hai góc và trong Hình 2 là 180o.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải

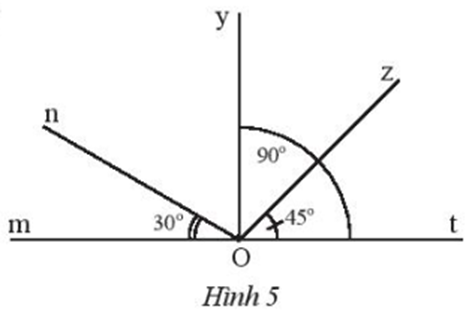
Ta có:
Vì hai góc và kề nhau nên:
Suy ra:
Vậy
Lời giải
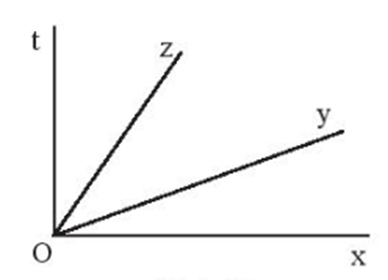
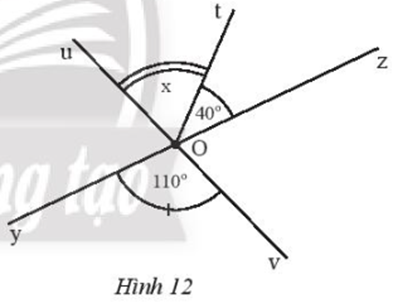
a) Ta có: và là hai góc kề nhau; và là hai góc kề nhau.
Vậy và là các góc kề với .
b) Vì tia Oy nằm giữa hai tia Ox và Ot nên:
Suy ra: .
Tia Oz nằm giữa hai tia Oy và Ot nên: .
Vì mà nên:
.
Vậy .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.