Bài tập Định lí và chứng minh một định lí có đáp án
21 người thi tuần này 4.6 1.4 K lượt thi 7 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 10
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 9
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 8
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 7
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 6
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 5
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 4
Bộ 10 đề thi cuối kì 2 Toán 7 Cánh diều có đáp án - Đề 3
Danh sách câu hỏi:
Lời giải
a) Ta có hình vẽ thể hiện định lí trên:
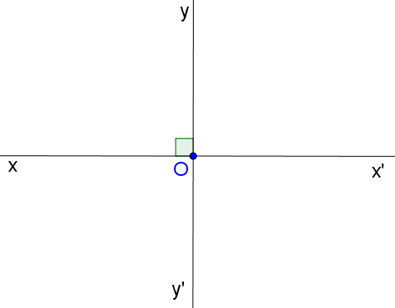
b) Giả thiết và kết luận của định lí.
|
GT |
Hai đường thẳng xx’ và yy’ cắt nhau tại O, |
|
KL |
Lời giải
* Giả thiết, kết luận của định lí:
|
GT |
, |
|
KL |

Lời giải
Định lí: “Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng còn lại”.
Ta có hình vẽ:
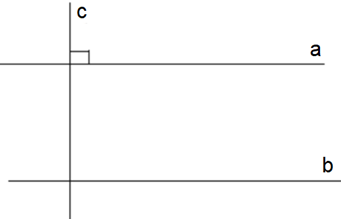
Giả thiết, kết luận của định lí:
|
GT |
a // b, c ⊥ a |
|
KL |
c ⊥ b |
Lời giải
a) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc so le trong bằng nhau.
b) Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Lời giải
a) Nếu một đường thẳng cắt hai đường thẳng sao cho có một cặp góc so le trong bằng nhau thì hai đường thẳng đó song song.
b) Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
Cách 2:
Nếu hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.